Menzerath-Altmann法則をRのnls関数で
Menzerath-Altmann法則(またはMenzerath法則; e.g., Altmann, 1980; 基本的アイデアはMenzerathが発見,Altmannが定式化)とは,ある言語学的単位の増加が,その単位の構成要素の減少に帰着すること。またはその逆。
もっと一般的にいうと,Altmann(1980)は,「ある言語学的単位の長さは,その構成要素の長さの関数である」としている。たとえば,ある形態素長(形態素内の音節数などとして測定する)の値が高ければ,その形態素内の平均的な音節長(音節内の音素の数などとして測定される)の値は低くなるということ。ある言語において,1音節からなる形態素の平均的な音素数は3,2音節からなる形態素(ひとつつあたりの)の平均的な音素数は2.5,3音節からなる形態素の平均的な音素数は2…というように。
それで,基本的にはさまざまな単位,たとえば時間などでもこの法則が当てはまるとされ,実証研究も少なくないし,ゲノムとかタンパク質とか,そういう分野にも応用されているんだそうだ。で,その関係は,簡単な方程式で表されると。
もっとも一般的な式は,
(a)
ここでのyは構成要素(小さい方)の長さ,xは対象とする言語学的単位の長さ,a,b,cは自由母数。eはネイピア数。この式を使い,観測から,a,b,cを推定する,というわけだ。
一番単純な方法だと,最小二乗法を使用することができる。
Rには,非線形最小二乗法用の関数nlsがあるので,これを使えばいい。Altmann(1980)にインドネシア語の形態素と音節の関係についてのデータが示されている。これは,こんな感じ。
Gabriel Altmann (1980). "Prolegomena to Menzerath's law". Glottometrika. 2: 1–10.
| Morpheme Length(Syllables) | Syllable Length(Phonemes) |
| 1 | 3.10 |
| 2 | 2.53 |
| 3 | 2.29 |
| 4 | 2.12 |
| 5 | 2.09 |
やってみる。
#データ入力 s<-1:5 m<-c(3.1,2.53,2.29,2.12,2.09) #可視化 plot(s,m,xlab="Morpheme Length",ylab="Syllable Length",pch=20,cex=2) #モデルをフィット fit<-nls(m~a*s^(-b)*exp(1)^(-c*s),start=list(a=3,b=0,c=0)) #サマリーなど summary(fit) AIC(fit) BIC(fit) #決定係数 cor(m,predict(fit))^2 #予測値をプロット plot(s,m,xlab="Morpheme Length",ylab="Syllable Length",pch=20,cex=2) points(s,predict(fit),col=2,pch=20)
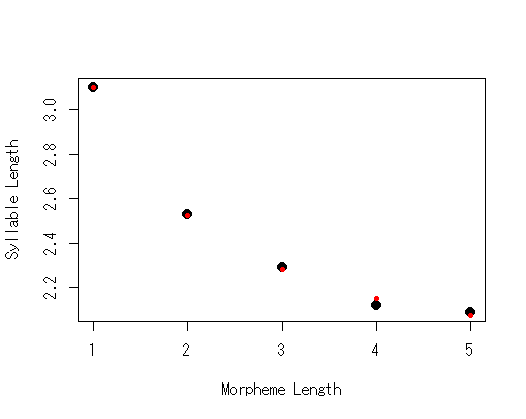
赤がモデル理論値。もちろん原著の推定結果ともほぼ一致している。
このデータでは,以下のようになった。
(b)
この法則がどれだけ法則と呼ぶに相応しい一般化可能性をもつかといった面と,具体的に(a)式がどれだけ観測にフィットするかということは置いといて,ある単位と,その構成素の関係に一般的な法則をもとめる姿勢というのは,とても正当な考え方だと思う。