【サドコマ⑦】まったくわからない統計が査読に回ってきたwww【査読者の責任】

英語教育研究の査読で困った!サドコマシリーズ第7弾!シェアしてくださると嬉しいです!
このシリーズについては↓
kusanagi.hatenablog.jp
このシリーズは,統計処理のTIPSや入門というよりも,査読時における両サイドのコミュニケーションについて扱っており,今回はその中でももっともコミュニケーションに関係が深い内容になります。
さて!査読をしているとき,査読を引き受けたものの,まったく馴染みのない統計方法が使用されていて困った!または逆に,投稿者側として,査読者が自分が使った統計に関してまったく知らない様子ままで査読されたようだ…という経験がある方は多いかと思います。
というわけで,第7弾は査読者の責任について私見を述べます。
*あくまでもこの記事は英語教育研究を前提にした草薙の私見であり,他分野,または統計学全般の規範とは異なる場合があります。
結論を先にいうと,査読において統計ないし手法上の観点で判断できないとき,メタ査読者に対して,「わからない」ということをありのまま告げることです。
問題の所在
まずは研究者自体が多様
英語教育研究(といっても,このブログの読者様の多くは他分野の方ですが…)は,その歴史的背景から見ても,そして現在の実態としても学際分野です。たとえば,英語教育に関わる学会は職能団体(つまり,ギルド)としての機能も備えていますが,そのメンバー全員が均質な訓練を受けているとは限りません。
小中高の教員免許は,一応制度上,業務独占資格に属しますが,英語教育の研究をしているからといって,必ずしも教員免許をもっているわけではありません。また,大学における教員は,実質的には修士以上の学位が業務独占資格のような位置づけこそ持っているものの,どのような専門性の持ち主であれ,大学の任用によって大学の英語教育に関わることができます。つまり,結局はさまざまな異なるキャリアの人の雑多な集まりというわけです。医学会みたいなものとは少し異なるわけです。
研究者,なかでも小中高における英語の教員養成に関わる研究者・大学教員に絞っても,文学・言語学を専門にする方(一般に内容学と呼ばれる),教育研究を専門にする方(一般に方法学と呼ばれる)の二分法による歴史的な区分があります。また,もう少し広げて英語教育関係者全体の出身学部を見ても,いわゆる教育学部,文学部,社会学部,国際関係学部,工学部…とさまざまですし,所属先として見ても,それこそ教育学部,文学部,社会学部…とまさになんでもあり!なわけです。
私個人はというと,地方国立教育学部出身で,ちなみに教育文化学部という名前でしたが,大学院は国際開発研究科という名前でした。この国際開発研究科は今は人文科学研究科に改編されたそうです。今,働いているところは,国際開発とは反対のような感じで,地域創生学部という名前です。ローカルになりました!でも改編前は人間文化学部国際文化学科でした。要は,教育,人間,文化,国際,地域など,時代によるラベルの流行り廃りは激しいけど,人間のコミュニケーションに関わりそうなところには大抵英語の先生がいるわけです。しかし,これは名前の問題だけじゃなくて,それだけ英語教育に関わる人はバラバラになっているってわけです。さらに加速度的にバラバラになるでしょう。
もう少し,突っ込んだ話をすると,しばしば批判となる大学の再編というのは,こうして学問のカタチをゴリゴリと変えていきます。英語教育研究が学際的というのも,実のところ自前のディシプリンというよりもこうした外発的で当座的な制度改革のしわ寄せによるところが多いと思っています。というか,いずれ間違いなく,そのように歴史的に語られるでしょう。
研究方法論の多様性
人間だけを見てもそのような状況ですから,人間の考え,特に研究方法論なんて厄介な代物になると,さらに多様になって当然ですよね。美しいことばを敢えて選べば「英語教育研究の研究方法論は実に多元的」です。あまり上品ぶらないでいえば,「研究方法論はもはや完全に断絶的な状況」ですし,ここにお酒を持ってくると私は3分後に「カオス!フリーダム!」と叫ぶでしょう,何度もだ。
パラダイムなどという便利な言い方もあって,教育研究ではしばしば以下のようなものが挙げられます。
このようなリストから英語教育研究者に好きに何かを選んでもらったとしても,それは多岐に渡るでしょう。私の個人的な経験として留保するにしても,上記のような考え方においてポジションが異なると,もうそれだけでほとんどマトモに話は成立しないのです。たとえば,私はある方向に強めの実証主義者の先生とはまったく話が合いません。話しても冷静ではいられません。もちろん,だからといってコミュニケーションを避けてはいけないのですが,お互いの無用な消耗を避けるために,ほとんど学会などでお会いしても議論を避けてしまうのが恥ずかしい現状です。
また,このような区別にも多分に問題があると思っていますが,いわゆる量的研究者と質的研究者も同じような関係にあると思います。そもそもお互いが冷静に議論するのは,ほとんど難しいのです。
さらに,もっと細かく研究方法論を見ていても,以下のような対立がいつも,どこにでも転がっているのが常態です。
- 実験系 vs. 質問紙調査系
- 実践重視 vs. 理論重視
- 頻度主義統計 vs. ベイズ統計
- 検定ベース vs. モデリング
- 機械学習/人工知能 vs. 還元できない人間の卓越性
- 教師あり vs. 教師なし
- 形式性(数式) vs. わかりやすい自然言語
ひどい場合は,アカデミックライティングの作法を巡って喧嘩が発生します。たとえば,
- 擬人化(the present study adopted...)するべき vs. だめ(In the present study, the author adopted...)
- パッシブライティングが正しい(the results were shown in ...)vs. だめ
- 一人称は使うな vs. 積極的に一人称を使うべき
といった対立があります。
要は,そもそもバラバラな集団なんだから,ありとあらゆるところに違いがあって当たり前って話なんです。まずはこの人種のるつぼ感を強く認識しないとなりません。
査読の問題に戻って
しかし,実際に査読の場面において,このような多様性・多元性が望ましい形で尊重されてきたか,といえばまったくそうではないでしょう。たとえば,国内の英語教育研究の一部のジャーナルは,ある特定のスタイルを,しかもそれが統計上の多数派でもないのに殊更重視し,そのスタイルに合わないものは一方的に除外してきたのだと思います。たとえば,強烈に実証主義的で,高度な統計分析を行っていて,擬人化して,パッシブライティングで,そして一人称を絶対に使わないで隠すスタイルが優れた研究であり,それだけが他のすべてに優越する唯一の規範で…といったような傾向があったかもしれません。
もちろん,査読システムとして,単一のスタイルだけを受け付ける方が弁別力としては向上します。低コストでもあるでしょう。そのような運用上のメリットとその必要性も十分にわかります。しかし,英語教育研究全体の実情を反映しているでしょうか。
また,査読者として自分に馴染みのないスタイル,研究方法,または統計がたまたま回って来たときに,自分が馴染みがないという理由によってそのスタイル自身や研究を否定したりするのは,このような学際的な分野の査読者としての責任を果たしているでしょうか?「知らない」(情報が少ない)=「駄目だ」(劣る)という構図は,差別の根本的なメカニズムだと教科書に書いています。
しかし,逆に査読者の責任とは,どのようなスタイル,研究方法,そして統計が来たとしても,適正に評価できる夢のような能力のことを表すのでしょうか?一体誰がそのような能力を持つのでしょうか?仮にそのような能力の持ち主がいたとして,ほぼ無償の査読をしてくれるでしょうか?
原則
というわけでは,私が考える原則はこうです。
- メタ査読者に対して,査読する論文がよくわからないことをありのまま告げること
まず第一の原則として,「査読者にとって馴染みがない」という理由は,学際分野に限っては「研究としての質が劣る」ことと切り離すべきだということです。「知らないから駄目」は,かなり均質な分野ではもしかしたら通じるかもしれませんが,まったく学際的な分野の実情に沿いません。なんなら,差別の構図に近いものがあります。
次に,「査読者にとって馴染みがない」こと自体も,逆に学際分野のことですから,査読者の無能力に帰されるべきではないということです。おそらく,英語教育研究全体を網羅的にカバーする学識の持ち主は存在できません。査読者は,せいぜいが読者を母集団としたときのサンプルの一部です。それも大概タダ働きの。
よって,よくわからない論文が回ってきたときに,査読者がすべきことは,編集委員などといったメタ査読者(meta reviewer)に正直にそのことを伝えるべきだということです。可能ならば,査読を引き受ける最初の段階で,意向を述べる機会があるならば,積極的に査読を辞退するべきです。
といっても,メタ査読者にとってすれば,それでも代わりの査読者が簡単に見つからない場合もあるでしょうし,日程の関係でそのようなことをいってはいられない場合もあろうかと思います。こういう場合は,何よりも査読の制度改革が必要だと思います。適切な査読者が見当たらずに,査読者が不可能だと申し立てる査読者に査読を強いる査読システムは端的にいってすでに破綻しています。
また,どうしても点数制などで点数をつけなければならないのなら,その項目(たとえば研究方法の適切性みたいな欄)は欠損で返すのがよいと思います。それで他の査読者の平均値などを代入するとよいでしょう。このときに,わからないという理由で低い点数,または高い点数をつけるのは憚られるべきでしょう。
もう少し,強い言い方をしてしまえば,(a)実際は査読できない場合に査読を引き受ける,(b)査読できないのにも関わらず一方的に低い評価をつける,(c)実質的に断れない査読を引き受けさせる…といった行為は,すべて研究倫理の領域に足を踏み入れていると思います。これらはマナーや技術の問題ではありません。研究者として資質が問われても仕方ない問題だと思います。ただし,これらも今後各分野にて少しずつ改善していくべきことだと思っています。
考えておきたいこと
しかし,ここでちゃぶ台を返すようなことをいってしまうと,よくわからない統計とか,よくわからない研究方法というのは,実際は書き手側のただの説明不足だったりもします。または,変に技術的にアピールしたいという意図があるかもしれません。私も過去にそのように思ったことが当然あります。新しい方法を手に入れると,人に見せびらかしたくなるものです。まったく,恥ずかしいですよね。結局,こういう側面があるから「わからないと落とす」ということに繋がります。
やはり書き手として大事なのは,査読者にとって馴染みがないこともその場で説明して伝える力だと思います。私はこれを,個人的に構成性と読んでいます。優れた論文は,一見まったく意味がわからなくても,順を追って読んでいくと,次第にこちらの知識が構成されていき,わからないことがその場でわかるようになります。そういう力を身に着けたいものですね。
サドコマシリーズ10箇条
…さて,と!新しいあいことばが増えました!
- 報告不備には生データ
- null resultsも評価する
- 検定の多重性は研究仮説を見る
- 有意じゃないとき効果量には言及しない
- 尺度水準や分布について必ず言明
- 事後分析をするなら検定を一切行わない
- わからない論文がきたらわからないという
次回は「有意差がないけど質的には効果があったかもっていうけど…」です。混合研究法について書きます!
私はSNSなどをやっておりませんので,どんどんシェアしていただくと幸いです!広くいろんな方に読んでいただけるよう一生懸命書いてます!
【サドコマ⑥】事後分析の恐怖【偽陽性】

英語教育研究の査読で困った!サドコマシリーズ第6弾!シェアしてくださると嬉しいです!
このシリーズについては↓
kusanagi.hatenablog.jp
量的研究法による英語教育研究が抱える最大の問題点の1つは,その偽陽性(false positivity)の高さにあると私は考えます。偽陽性とは,実際には有意ではないのに,研究結果として有意となることです。仮にそれが指導法の効果検証だとしたら,効果がない指導法を社会に対して派手に喧伝してしまうことになりかねません。そして,この偽陽性は,俗に事後分析(post-hoc analyses)と呼ばれる一般的な研究慣行によって飛躍的に高まります。しかし,英語教育研究において事後分析は,このような危険性に反して,むしろ丁寧で優れた分析とみなされ,推奨されることもありました。ここに研究規範に関する一種の矛盾があります。一体,私たちは事後分析をどう捉えるべきなのでしょうか?…というわけで,第6弾は英語教育研究における事後分析について私見を述べます。
*あくまでもこの記事は英語教育研究を前提にした草薙の私見であり,他分野,または統計学全般の規範とは異なる場合があります。なお,この記事は,すでに学術論文として刊行された草薙・田村(2017)*1の内容を参考にしています。
結論を先にいうと,私自身はいわゆる事後分析について強固な反対派であり,ここで提案する方針は「事後分析をする場合は検定を一切行わないこと」です。
問題の所在
偽陽性
新型コロナウイルス感染症の拡大によって広く社会に知られるようになったことですが,臨床検査,そして統計的帰無仮説検定には以下の4種類の場合が考えられます。ここでは,平均差の検定を例に取ります。
| 実際に差がある | 実際には差がない | |
| 検定が有意 | 真陽性(true positive) | 偽陽性(false positive) |
| 検定が非有意 | 偽陰性(false negative) | 真陰性(true negative) |
統計学の文脈では,偽陽性の場合を第一種の過誤(type I error),偽陰性の場合を第二種の過誤(type II error)と呼びます。また,計算上第一種の過誤が起こる確率をαとし,これを危険率と呼びます。有意確率も同じです。また,同様に,第二種の過誤が起こる確率をβとします。一般に,第二種の過誤は起きないにこしたことがないですから,「第二種の過誤が起きない度合い」を考えて,1-βという確率を考えます。これが,いわゆる検定力(power)や検出力と呼ばれるものです。
一般に,第一種の過誤が起きる確率を減らそうとすると,逆に第二種の過誤が起きる確率は増えてしまう関係にあります。計算上,αと1-βは標本規模に大きく依存しますから,一定の効果量などを参照基準とした上で,予め定めたαと1-βを満たす標本サイズを見積もることができます。検定力分析(power analysis)と呼ばれる手続きです。
広く様々な分野で知られる統計改革(statistical reform)後,特に日本の外国語教育研究では,2010年代のメソドロジー・ブーム(草薙他,2021*2)のとき,検定力分析にもとづく事前の標本規模決定が推奨されましたが,英語教育分野全体として見ると,定着にはほど遠かったといえると思います。つまり,現状においても相対的多数の英語教育研究は検定力分析を使用していません。
さて,必ずしもすべての英語教育研究がそうであるわけではないですが,英語教育研究,特にその指導法効果検証ではしばしば検定結果と指導法の効果が対応付けられます。典型的には,平均差の検定が有意であれば,指導法に効果がある,有意差が得られなければ指導法に効果がないという関係です。ですから,上の表を,
| 実際に効果がある | 実際には効果がない | |
| 検定が有意 | 真陽性(true positive) | 偽陽性(false positive) |
| 検定が非有意 | 偽陰性(false negative) | 真陰性(true negative) |
というように書き換えられます。一般に検定が有意であれば,パブリケーション・バイアスによって論文が公開される確率は高まります。非有意であれば公開されにくくなります。査読で落ちるからです。さらに,偽陰性(の結果が広まること)はそれほど英語教育実践上,致命的ではないと考えられます。とういうのも,非有意であれば,当該の指導法が社会に流通したりする機会は減り,その点では確かにロスがありますが,なにせ,実際に効果があるのですから。一方,偽陽性の方が私は深刻だと考えます。実際には効果がない指導法が効果的な指導法として,より流通する機会が増えるかもしれません。これは端的にいって,社会的損失ですから研究者の責任は極めて重いと思います。
いつも申し上げているように,世界中の言語教育に関する年間の研究総数を考えるとそれはもう莫大な数になりますから,すぐに思いつくようなすべての指導法,学習方法,指導技術,または方略であれ,どこかの研究によってすでに有意差が報告されていると考えます。「有意差が過去の研究にて報告されたことがある」という基準をエビデンスと呼ぶのなら,私はほぼすべての指導法,学習方法…にはそういう限定的な意味でエビデンスがあるのだと考えます。一方,エビデンスというのは,私は2値的に,つまり「ある」「なし」で語られるべきだとも考えません。意思決定の一つの方針だと捉えています。
事後分析
事後分析(post-hoc analyses)は定義が難しいものです。一般に以下のような特徴をもつと考えます。
- 研究仮説(RQ)に含まれない,または研究仮説と整合的でない分析を加える
- 複数の研究仮説があり,研究仮説の中に仮定や条件がつけられている場合にのみ分析を加える
- 一論文において実験・調査の分割がされている
1の場合の例です。群間比較計画によって指導法の効果検証をしたあとに,「男女やクラスによって効果に違いがあったか」を検証するために,標本分割を行って再度検定をかけるが,これはRQは記載されていない場合などです。しばしば,結果(results)ではなくて,議論(discussion)の章に書かれている場合もあります。
2の場合は,RQが特徴的ですので見たらわかります。RQが複数並んでおり,主に2つ目以上のRQにおいて,if-then命題が含まれています。RQ1が「効果があるか?」,RQ2が「もしも効果がある場合,それはどのような標本にとって?」のような形式や,分析に着目すると因子スコアの差を検定したあとに,各項目間の検定をもう一度網羅的に行うような場合です。さらに多くの場合,「どのような項目において~」というようにhow, whenといった疑問詞を伴います。
3の場合は,Study 1,2,3...というように書かれていたり,Experiment 1,2,3...というように書かれています。これ自体が悪いというわけではありませんし,これによって事後分析であるというわけではありません。むしろ,ポイントは,Study 2やStudy 3が,Study 1から得られた知見がなければ成立しない計画になっているような場合です。極端な場合,2と3の区別はつきません。章立てや論文の構成の問題だけの場合もあります。
いずれにせよ,これらのポイントは,当初計画していない分析,つまり結果が出たあとに分析を加えている点なのです。これはプレレジとして知られる事前登録制度の方針の,まさに反対の行為なわけです。また,一般にQRP(quetionable research practice)の1つとして考えられているHARKing(結果を既知とした仮説形成)と区別ができません。1の場合は形式的にはHARKingではないのでしょう。仮説がないがまま分析をしています。どちらかというと,ただ形式的にRQとして言明していないだけです。2や3は,HARKingなのかそうでないのかが判断できません。本質はすべて実際は探索的な研究を形式的に検証的に見せる研究慣習です。いうまでもなくこれが,私個人がもっとも英語教育研究の発展を妨げていると睨んでいるもので,そしてこのシリーズ,サドコマに通底するテーマに他なりません。
ところで,具体的にこのような研究がどのような分析を行うというと,草薙・田村(2017)は,以下の3つを挙げました。
- 標本分割:あらゆるデモグラフィック変数によって,標本をサブグループに分割する
- 分析の平行化:あらゆる種の研究者の自由度によって,複数の分析を同時に行う(当然cherry-pickingにもつながる)
- 効果のデータマイニング:予めRQにて言明しないアウトカムの効果検証を行う
ここではそれぞれの紹介は避けますが,すべて,偽陽性を爆発的に増加させます。この問題は,私がすでに何度も述べていることにも関連します。
kusanagi.hatenablog.jp
kusanagi.hatenablog.jp
特に後者の記事を読むと,系統的にcherry pickingなどを行うことによって,上記の3つを組み合わせて有意差を技術的に発見することは容易であることがわかります。「有意差を発見する」…。統計学をかじったことのある人にとってはすごいパワーフレーズです。
中でも厄介なのが,そしてもっとも頻繁に見られる例ですが,熟達度といったデモグラフィックデータによって標本分割を行い,つまり上下群によって分割して効果検証を再度行うことです。これは,単純に平均への回帰によって,下位群が常に有意差を得やすくなります。このようにして,「下位群によりよく効く指導法」が生まれてきます。しかし,これも偽陽性に過ぎないと考えるのが自然でしょう。
しかし,このような危険性を抱えるものの,事後分析は特定の分野,特定の世代,特定の研究者において,危険な研究行為であるどころか,逆に規範とされてきました。いってしまえば,これこそがよい論文を書くためのテクニックだったのです。私も,主に2010年代の日本で研究トレーニングを受けたキャリアでしたが,このような分析手順を聞くことは少なくありませんでしたし,なんなら実際に行ったことがあります。もちろん,英語教育研究に限った話ではまったくありません。そして,未だに,このような研究行為を規範とされている研究者も数多く知っています。いわく,「データを丁寧に見て」,「より情報量のある分析を行う」といった趣旨です。私も査読者から何度も叱られたことがあります。「データを丁寧に見ると色々わかってくる」「草薙はデータを大事にしていない」と。
もちろん,私はデータを大事に見ることに反対しません。しかし,それはあくまでも探索的な研究であって,仮説検証を伴う検証型の研究の規範ではないということです。データを得てから仮説生成をすることは,まったく悪くありません。逆に素晴らしい研究になると思います。問題は,それらを履き違えることです。何度も書いているように統計的帰無仮説検定は,あくまでも検証型の方法なのであって,これを探索的に使ってしまうと大失敗する,ということです。この辺は,多重検定の回にて詳しく説明しています。
原則
というわけでは,私が考える原則はこうです。
- 事後分析をする論文は検定を一切行わない
前述の通り,本質的に探索的な論文は,統計的帰無仮説検定にまったく適しません。統計的帰無仮説検定を行わければ,上記のような偽陽性の問題は原理的に発生しないはずです。ですから,事後分析が見られ,さらに統計的帰無仮説検定を行っている(ほとんどの場合,多用していますが…)場合に査読者がすべきことは,検定結果を掲載せずに,探索的な論文としての相応の記述を求めることだと考えます。適切な記述統計の報告,可視化等に留めて,その傾向から派生する新たな研究仮説を研究者コミュニティにて共有することがよいでしょう。
また,サラミ出版の問題とも関連するため非常に難しいのですが,事後分析を行っている論文は,1論文ではなくて別論文として投稿するよう求めることも場合によっては考えられるかもしれません。
考えておきたいこと
もちろん,探索的な研究の場合,生データの共有は常に重要です。また,この問題も括ってしまえば,「従来,探索的な研究を正当に評価する枠組みが存在しなかった」という業界に根ざす状況の帰結と言えるかもしれません。今後,検定を行わない研究,研究仮説を持たず,逆に研究仮説を生成する研究をどのように評価するか,といった学会全体のムーブメントが必要になろうかと思います。
なお,ベイズ統計など,従来の頻度主義的な検定の代替方法についても関心が高まっています。もちろん,これらの方法はp値とは無縁ですが,私は本質はあくまでも変わらないと思っています。ベイズ統計を使ったら,事後分析が好きなようにやり放題だとか,少なくとも本質的にはそんな馬鹿な話はないと思います。むしろ大事なのは,探索的な研究と検証的な研究の区別であり,それらの両方を,適切に評価し,活用していく科学的リテラシーそれ自体なのだと信じます。
もう1つ考えなければならないのは,研究規範の相違についてです。私がこのサドコマで述べている方針も所詮,冴えない一研究者である草薙の考えに過ぎません。未だにここで述べた事後分析こそが優れた規範,特にパブリケーション上の重要テクニックであると主張される方は大勢います。もしかしたら主流派かもしれません。このような規範の違いが起きたとき,私たちがすべきなのは,やはり話し合いなのだと思います。私は,私の考えが広まることよりも,話し合いのきっかけになることを希望しています。査読というのも,まさにその場なのだと思います。
サドコマシリーズ10箇条
…さて,と!新しいあいことばが増えました!
- 報告不備には生データ
- null resultsも評価する
- 検定の多重性は研究仮説を見る
- 有意じゃないとき効果量には言及しない
- 尺度水準や分布について必ず言明
- 事後分析をする論文は検定を一切行わない
次回は「まったくわからない統計が査読に回ってきたwww」です。査読者の責任とコミュニケーションについて書きます!
私はSNSなどをやっておりませんので,どんどんシェアしていただくと幸いです!広くいろんな方に読んでいただけるよう一生懸命書いてます!
*1:草薙邦広・田村祐 (2017) 「外国語教育研究における事後分析の危険性」『外国語教育メディア学会中部支部外国語教育基礎研究部会2016年度報告論集』30-49.
*2:草薙邦広・石井雄隆・中村大輝・雲財寛・李在鎬・熊井将太・山森光陽(2021)「統計改革は各教育分野にどのように展開していったか」第63回日本教育心理学会総会. オンライン開催.
【サドコマ⑤】それ正規分布しなくない?【尺度水準と分布】

英語教育研究の査読で困った!サドコマシリーズ第5弾!シェアしてくださると嬉しいです!コロナ禍や所属先が変わったりして,しばらくシリーズが放棄されていました!しかし,少数の熱心な読者さまの励ましとお叱りの末,ここから少しずつ再開します!
このシリーズについては↓
kusanagi.hatenablog.jp
英語教育研究を巡る査読のやりとりでは,「このデータは正規分布には従わない(から分析は間違いだ)」,「このデータはそもそも順序尺度である(から結論は信用できない)」,「尺度水準を間違えて扱っている(から落とす)」といったやりとりが多く見受けられます。私はこの点についての相談を頻繁に受けますが,論文の書き手側も査読者側も,尺度水準や分布に関するコミュニケーションに不安を覚えていらっしゃるようです。この点についてあまりコンセンサスとなるべきような点も見当たりません。…というわけで,第5弾は予定の内容を差し替えて,英語教育研究における尺度水準の取り違えと分布の無視について私見を述べます。
学際的分野である英語教育研究が,研究実践において取り扱うデータは実に多様です。しかし,現在主流であるデータ分析方法は,正規分布を仮定した分析がほとんどです。正規分布以外の分布に従うデータを取り扱う分析方法も普及の過程にありますが,そもそも英語教育研究では,確率分布に関する基礎的な知識が慢性的に欠落しているといわざるをえません。ここでは査読時を念頭に置いて,データの尺度水準や分布について疑問が起きたとき,どのようなコミュニケーションが研究を改善するために有効かについて考えます。統計分析の技術論というよりは,査読時のコミュニケーションに着目しているのがこのシリーズのコンセプトです。
*あくまでもこの記事は英語教育研究を前提にした草薙の私見であり,他分野,または統計学全般の規範とは異なる場合があります。
結論を先にいうと,私が提案する方針は「尺度水準や分布に関する言明を必須とすること」です。
問題の所在
尺度水準
他の多くの統計分析を使用する研究分野と同じく,英語教育研究においても,スティーブンズの尺度水準が常識とされてきました。たとえば,英語教師向けのデータ分析入門書である「英語教師のための教育データ分析入門」(三浦他, 2004)では,非常に平易に,身近な例を含めて,そして丁寧に尺度水準について解説しています。それ以降の外国語教育研究に関する類書も同様の取り扱いをしています。スティーブンズの尺度水準は,
- 名義尺度
- 順序尺度
- 間隔尺度
- 比例尺度
という分類です。ここではそれぞれについて細かな解説を省きます。
近年では,通例的に,
- カテゴリカルデータ(名義尺度に対応)
- 順序データ(順序尺度に対応)
- 量的データ(間隔尺度・比例尺度に対応)
などということもありますし,変数として見る場合は,カテゴリカル変数とか量的変数という場合もあります。その他にも,ときに,
- 質的データ(名義尺度・順序尺度)
- 量的データ(間隔尺度・比例尺度)
と表現するときもあるようです。さらに同じ変数として見るとしても,やや少し見方を変えて,
- カテゴリカル変数
- 離散変数
- 連続変数
として区別する場合もあります。
いずれにせよ,これらは2つ以上の値に成立する演算または関係性(2項関係)によって分類しているものだということを意識するとよいでしょう。たとえば,ちょっとだけ厳密に見てみましょう。
名義尺度について考えると,で,
だったら,これは反射的であり,
かつ
だったら対称的であると考えたりするわけです。または,順序尺度は,
で
なら非対称的であって,
が成立するので,推移的です。間隔尺度では,
,
,
,
が成立する(加法性)とか,比尺度では,さらに
となるような
(乗法単位元,0など)があるといった具合です。
要は,尺度水準によって適用してよい演算と適用できない演算があるわけです。たとえば,「男性」,「女性」といった値を取るだろう名義尺度なりカテゴリカル変数とみなすところのものは足したり引いたりできません。ただ単に(男性は男性)で,さらに
(男性は女性じゃない)というだけの話です。
しかし,英語教育研究ではこのようなことが十分に周知されていないことが事実としてあるようです。
分布
実は,英語教育研究が利用するデータの多くは,常識的に考えると正規分布とみなすには問題を抱えています。むしろ,逆にどのようなデータが正規分布らしいかというと,当然,最初から正規分布に従うように加工されたデータです。たとえば,
- 項目反応モデルなどで推定された能力値や,それに派生する標準テストの得点
- 予め尺度構成された質問紙の因子得点や,それに準ずる合計尺度得点
などが典型です。要は,複数のデータを足し合わせたりしてできた二次的なデータです。一方,それ以外の,英語教育研究に頻繁に見られるさまざまなデータについて考えてみます。
- 正答 → 0/1のカテゴリカルデータ
- 正答数 → カウントデータのため,そもそも連続変数とみなしにくい
- 正答率 → 0以上1未満であり,さらに天井効果,床効果が多く見られる
- 時間(反応時間,回答時間,読解時間…) → 裾が右に流い分布型となることが一般的
- 回数(提出回数,出席回数,ログイン回数,使用回数,頻度…) → カウントデータ
といったように,少なくとも正規分布や,または間隔尺度以上であるとすらみなしにくいことが明白なものが多いのです。

また,前述のように,正答率は天井効果や床効果が起きることが多いですが,教育に関わる限り,集団基準準拠テストでもなければ起きて当然のことです。同様に,教育というドメインに由来することとして,切断効果も挙げられるでしょう。特定の基準によってすでに選抜された集団を対象にデータを取ると,分布が歪んで当然です。たとえば,ある大学の新入生,その4月の学力データを取ると,合格ライン以下の得点をもつケースは合理的に考えて少ないはずです。さらに,双峰性などとも呼ばれますが,英語教育研究では,2つ以上のピークを持つデータを得られることも少なくありません。得てして,異種のサンプルが混ざり合うことによって発生します。たとえば,小学校のデータを対象とすると,「英語塾に通っている学生」vs.「通っていない学生」といった具合です。しかし,学級を対象としたデータではこういった状況が自然に発生します。
さて,ここまでの話を簡単に,そして乱暴にまとめてしまえば,英語教育研究のデータの圧倒的大多数は,そもそも正規分布には縁遠いのです。まずはここを前提として進めなければなりません。かつて,私に「なぜか私のデータっていつも正規分布しないんです。私の行いが悪いのでしょうか?」と相談をくださった方がいました。普通にデータが回数だったので「当たり前ですよ」とお答えしたら,「やはり!?お祓いとか効きますか?!」といわれました。
目的をもって選ぶことと現実
さて,英語教育研究の多くのデータは正規分布には縁遠いといっても,私は「正規分布を前提とする分析による結果はおしなべて間違いだから唾棄すべき」という論に与することもなければ,「これからは正規分布を前提とする分析ではなくて,難しいナントカモデルを学ばなければならない」といった論に偏るつもりもありません。もちろん,データに対してより適切な確率分布を仮定した分析は有効です。しかし,逆に,目的によっては正規分布を前提とした分析も同等に有効だと考えるからです。
ここで,こんな話を考えてみましょう。私は世でいうところの大男の部類でして,183cm,今朝測ったら92kgありました。なので,日本のメーカーが作った服だったら,大抵サイズ表記でLかXL,そのときの流行りと私の太り具合によってはそれ以上の製品を手にとります。少し前,若い世代にオーバーサイズファッションが流行したときがありました。このとき,私が服を買いに行くと,明らかに小柄な20歳くらいの女性が,私のような大男と並んでメンズのXLのセーターを手に取ったりしていました。
おそらく彼女は「オーバーサイズで着る」という明確な目的をもっています。そして,おそらくこのときの風潮や彼女の嗜好からすると,ウィメンズのSよりも,メンズのXLが実際に似合うのだと思います。しかし,それでもけっして,彼女の身体は私並に大きくなったわけではありません。
話をもどして,私は合理的には正規分布にフィットしないデータに対して,正規分布を仮定するという選択は特定の研究目的の下で正当化されるべきだと考えます。しかし,その選択と目的自体は十分に論文において周知されるべきであると考えます。
逆に私が問題だと考える点は,前提の逸脱ではなくて,前提を逸脱しているということの留保のなさと未周知なのです。オーバーサイズファッション自体は悪くありませんが,オーバーサイズで着ると,着用者のサイズはほとんどわからなくなります。ここに致命的な情報の損失があります。ファッションならまだしも,研究がこれでは困ります。なんでもかんでも正規分布だと盲目的にみなすと,もともとどのようなデータなのかがわからなくなります。データへの無関心を助長します。さらに理論的にいっても,正規分布の逸脱が及ぼす結果・推論への影響がわかりません。
ですから,ある程度「寸法から大きく外れた,メンズのXLを着ている」という留保が必要なように,どのような尺度水準と分布かを予め言明する必要があります。
原則
私が考える原則はこうです。
- 扱うデータに対して尺度水準と分布を明確に言及する
- 査読者はあくまでも研究の合目的性に照らし合わせて,そのことを追求できる
たとえば,「本研究では,アウトカムであるXテストの得点を間隔尺度と捉え,正規分布に従う確率変数であるとして扱った」などと論文内において記述すべきだと考えます。できれば,その理由も添えるとなおよいでしょう。「2群の平均差の検討のために十分である」といった具合です。私はこのような記述をしたとき「当たり前で冗長だから不要である」という指摘を査読者から受けたことがあります。しかし,私はそう思いません。あくまでも,研究者の説明責任の範疇に含まれると考えます。
同様に,査読者は「実際にどの分布を仮定することが最適か」という技術論よりも,あくまでも応用分野ですから,研究との合目的性に照らし合わせて理由を追求するべきだと考えます。つまり,査読者のおしごとは,たとえば「正規分布じゃだめ!」という指摘よりも,「なぜ正規分布を?」と尋ねて説明を求めることです。
ときに「何分布を仮定することが現状の技術水準において最適か?」といったことが話題になることもありますが,これは英語教育研究といった応用分野ではそれほど大きな問題ではないと私は思っています。もちろん私は個人的に関心がありますが,そのようなことを一論文の査読の場で争わなくてもよいかと思います。大事なのは,その研究の目的と分布を選択したことの関係性です。
考えておきたいこと
もちろん,これまでも何度もこのシリーズにて述べているように,生データの共有は非常に重要です。また,適切にデータを可視化して共有することも常に基本の座を占めるでしょう。さらに,この記事は適切に分布に合わせたモデリングの重要性を貶めるものではありません。
むしろ,データ自体の共有,可視化,適切なモデリングへと至るための布石として,尺度水準や分布に関する言明が査読を巡る科学的コミュニケーションの上で機能的に重要だと考えています。たとえば,「なぜ正規分布?」と査読者に問われることによって,その証拠としてデータそのものを可視化したり,分布について検討する機会自体が相対的に増えるでしょう。また,正規分布の仮定が目的に合致しないのならば,別の分布を仮定したモデリングを行うイニシアチブが増します。このようなやりとりは研究を漸進的によりよくすると期待できます。
さて,そもそも,この話の根本について考えると,それは英語教育研究の研究方法論史から理解することもできます。戦後の英語教育研究は,心理学の研究方法論を規範として発展してきました。たとえば,心理学における各種の尺度構成やテスト理論は正規分布に従うデータを得るための非常に優れたツールです。しかし,英語教育研究は学際分野ですから,心理学の研究方法論を心理学ではあまり取り扱わないデータに対しても過剰適用するようになりました。たとえば,言語学・応用言語学に由来する回数データ,頻度データなどは,あまり心理学では扱いません。さらに,近年では教育工学・情報学との関連から,オンライン学習履歴が使用されるようになりました。これらの分野ではそもそも機械学習などが盛んに使用されていますが,英語教育研究では,このような,ときにビッグデータなど呼ばれるデータに対しても,依然として心理学由来の研究方法論を過剰適用している例が見られます。つまり,学際化の中で方法論的なミスマッチが起きているのです。このような学際化の末,英語教育研究ではどのような研究方法論が発展するのでしょうか…なんて。
サドコマシリーズ10箇条
…さて,と!およそ二年越しに新しいあいことばが増えました!
- 報告不備には生データ
- null resultsも評価する
- 検定の多重性は研究仮説を見る
- 有意じゃないとき効果量には言及しない
- 尺度水準や分布について必ず言明
次回は事後分析について書きます!今回は軽めでしたが,次こそは重めの自信作です。
私はSNSなどをやっておりませんので,どんどんシェアしていただくと幸いです!広くいろんな方に読んでいただけるよう一生懸命書いてます!
英語教育系学会における会員の年齢構成
学会における年齢構成問題
私は,昨年共著者らと執筆した『英語教育のエビデンス』という本の中で,何度か英語教育を担う人材の年齢構成について触れました。簡単にいってしまえば,学会などの集団をサンプルにすると,若手会員が相対的に少なく,中堅・ベテランの方が会員数が多いという状況になっているということです。そしてこの傾向は年々強まっていきます。もちろん,別にこれは何も英語教育だとか,英語教育系学会に固有なことではなくて,日本におけるもっとも一般的な年齢構成の必然的な帰結だと思います。
このような視点をもって,各学会・研究会は若手支援やら会員の拡充についてさまざまな取り組みを行っています。私も上記の本において,多少若手支援の取り組みについて情報を提供しました。
「草薙くん,いや学会はむしろ発展しているからね?」
そこで驚いたことに,このような私の(そして大勢の)見方とは異なり,現在も英語教育系の学会は会員数が増えており,むしろ順調に発展しているという反論を少し前に頂きました。いわく,当該の私の記述が,「過度に悲観的な見方を持たせようとして根も葉もないことを扇動的に書いている」といった種のご批判です。
まず,第一に重要なことは,「会員数が仮に増えていこうとも,それはボリュームのある世代が現状において退会されていないだけで,大量退職が起きて急激に会員数が下り始める」ということです。要は,重要なのは会員数ではなくて,繰り返し書いているようにその年齢構成なのです。
もう一つは,やはりデータを基に議論するのがよろしいかということです。ちょうど,素晴らしいことに中部地区英語教育学会(CELES)が,今年度,設立50周年記念誌*1
を発行されたようです。関係の先生方,大変お疲れさまでございます。中部地区英語教育学会(2022)では,pp.244 - 248に,1971年から2021年度までの一般会員数,学生会員数のデータを所蔵しています。これを打ち込んで,可視化してみます。
中部地区英語教育学会の一例
可視化するとこうです。縦軸が会員数,横軸が年代です。青が一般会員数,緑が学生会員数です。年度によって報告されてなくてデータがないときがあります。
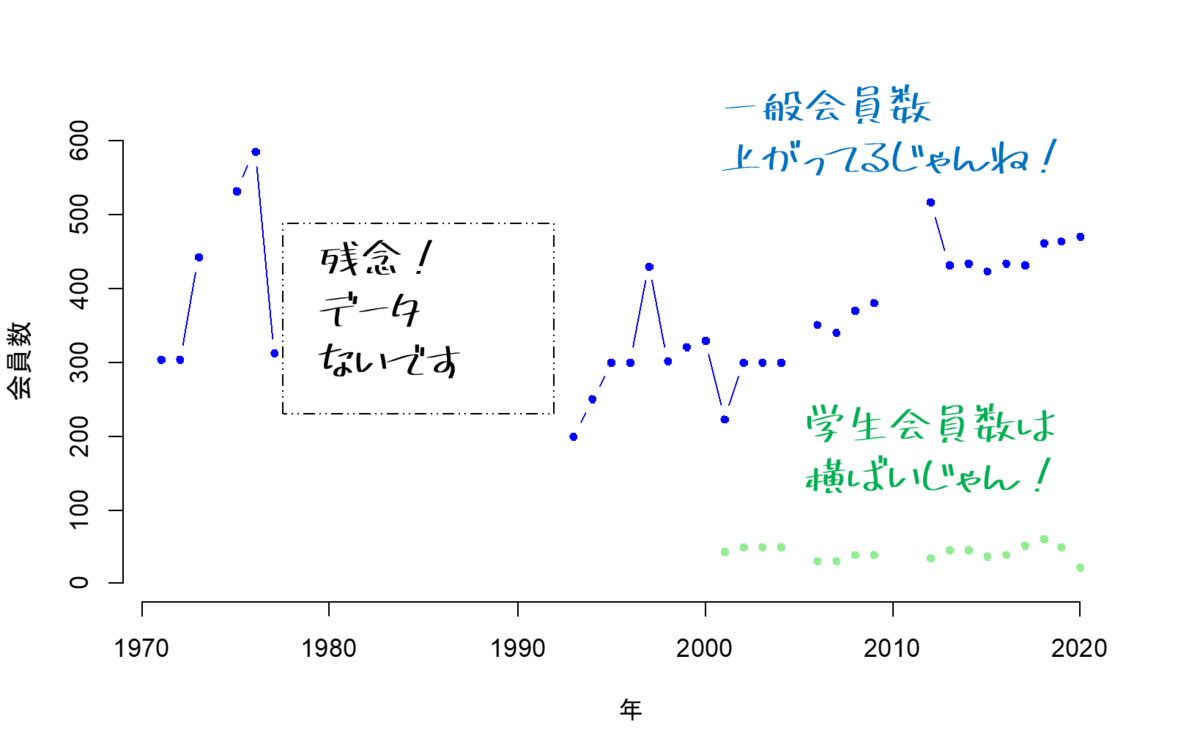
たしかに,一般会員数は右肩上がりに見えます。それに学生会員数も横ばいに見えます。
しかし,学生会員比率はどうでしょう。
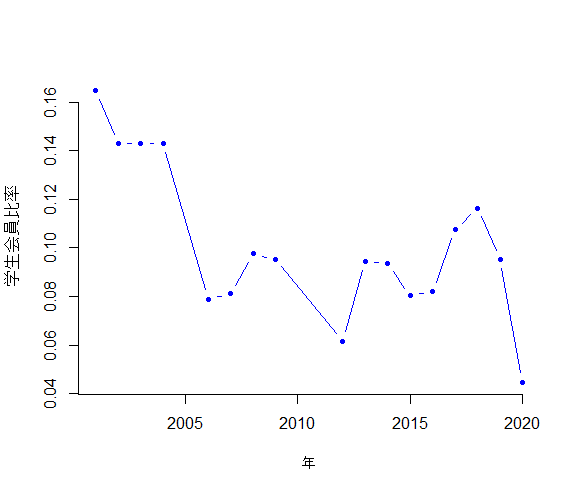
これは右肩下がりのように見えますよね。2010年代に入ってからは10%を切っていますね。
扇動的?
扇動的といういわれは受け入れるとしても,それほど根も葉もないことを思いつきでいっているわけではないということがわかるグラフかと思います。
*1:中部地区英語教育学会(2022)『設立50周年記念誌』中部地区英語教育学会.
『英語教育のエビデンス』に頂いたコメント
『英語教育のエビデンス』
2021年度はコロナ禍もあり,所属組織が変わったりなどといっているうちに,すっかりこのブログからも手が離れてしまいました。この間に,研究社から私も複数章執筆した『英語教育のエビデンス―これからの英語教育研究のために』が出版されました。
私は以下の章を担当しました。
- 第一章「英語教育研究の新たな原則―エビデンスについて考える前に」
- 第八章「測定モデルと共通変数を問う―PK-Testを事例に」(工藤洋路先生と分担執筆)
- 第九章「これからの英語教育研究のあり方を考えて」
『英語教育のエビデンス』へのコメント
幸いなことに,私を含む著者らが思っている以上に多くの方が手に取っていただいているようです。著者陣の中では比較的無名というか,一番の若手である私のところにすら,相当数のコメント,感想,質問などが届いて,とてもびっくりしました。先日も関東甲信越英語教育学会のオンラインイベントでも,座談会としてこの書籍について取り上げてくださり,その中で直接的に質問を頂いたりしました。
私は,自分から「誠実な方だ」というには憚られるような輩ですから,それぞれこの本に関して頂いたコメントに対して,これまで十分にお答えできていませんでした。もちろん,私の不徳のなすところです。しかし何より,そのときは「自分でもどう答えるべきかわからなかった」ということも多かったのです。
ですが,ちょうど出版後からも時間が経ち,自分の考えも少しずつ固まってきました。そこで,このようなブログの記事にでも書いておいて,個別にお答えできなかったコメントを成仏させたいというか,むしろ整理のために文章化しようと考えました。さらに運良くこれがお目に留まっていただければ,などと欲張って。
ここで頂いたコメントの中で主要な3つをピックアップし,それに対する私の考えを書きたいと思います。最初に申し上げますが,まだお手にとってられない方や,教育現場のレベルの議論にのみ関心を持つ方を読者として想定しておりません。大変な失礼をいたします。
①第一章がむずかしいから一瞬で読むのやめた
一番多く頂いた反応がこれです。これは単純に私の力不足です。共著者の先生方にも,端的に申し訳ないと反省しています。
ですが,書いてあること自体,そして論立ての仕方については,私は自分の力不足を感じません。私は非常に内向的なので,「なんでもひどく後悔ばっかりしている」タイプで,いうなら「過去に自分書いたものはすべてクソだからすぐに燃やしてしまえ」という趣の焚書オジさんなのですが,この章については奇跡的にそう思っていません。おこがましいですが,私は珍しく私の持つものを出せたと思って自己満足しています。
そして何よりも以降の章を読むためにも,そしてこの本の趣旨を理解するためにも重要な章であると思っています。
もし読みにくいようなら,他の章といったりきたりされると少しわかりやすいかも…などと思っております。おいしい刺身というよりは,スルメやエイヒレをイメージいただけると幸いです。無責任な態度ですけど。
さらに関心を持っていただけたのでしたら,以下の論文と合わせて読んでいただけると私が大変喜びます。
②しょうもない研究ならしないほうがマシ?
私が担当した第九章に,エビデンスを「つくる」ための工夫,特に学会が取り組むべき方法の1つとして,研究テーマの緩やかな集中戦略を挙げました。要は,100人の研究者が100個の独自の研究テーマに取り組み,研究規模(予算,それによるデザイン)の問題によって,主に政策レベルのエビデンスがつくれない状態よりも,100人の研究者のコストを10個の研究テーマに集中させたほうが,エビデンスを「つくる」という目的に合致しているといった論です。
これは,一般に経済学や行政では,選択と集中と言われ,殆どの場合,悪評をもって語られます。ですが,それでもあくまで日本の英語教育研究を念頭に置くなら,研究組織の規模の拡大はエビデンスを「つくる」ためには,もちろん今でも有効だと考えています。
ですが,このような記述は,個人による小規模な研究を暗に否定し,主として大規模な組織的研究に参加しない(できない)研究者,そして教育実践者が個人の関心によって自発的な研究を行うことを抑制しないかという懸念が生まれます。「エビデンスの本を読んだら,研究が怖くなった」といった,要は萎縮につながるのでないかということです。このような反応が非常に多かったのには私も当惑しました。
この点については,第一に,私に限らず著者一同は,この本によって,英語教育研究をすることに関して,萎縮させたいわけではまったくありません。小規模の,そして個人の関心や都合に基く研究はこれまで通り,またはこれまで以上の価値を持つでしょう。ですが,あくまでもエビデンスに関していうならば,これにはおよそ関わらないままでしょう。
しかしそもそも,研究はエビデンスを「つくる」ためだけのものではないのです。実践者としてのQOL,個人の知的充足,組織内での業績評価,アカデミアの評価,人材保証,人事評価,そして何より人材育成…研究はありとあらゆる複合的な社会的機能を持っています。研究者と実践者はこれらの複合的な文脈と目的をもって研究します。著者らはこのような現状を批判して,一部の,たとえばエビデンスに関わる研究のみに価値があるとして,それ以外の研究者の居場所をなくしたいわけではありません。
しかし,一方でこのような複合的な文脈があるのだからこそ,私は「しない方がマシ」な研究も実際に数多くあると思っています。エビデンスに関わらない研究は無意味というわけではないですが,端的に研究倫理の観点からの問題も意識しないといけないと考えているからです。
多くの教育研究は「人間を対象とする研究」に相当します。英語教育研究のほとんどには,明確な身体に関する侵襲性はあまりないですが,個人情報の観点における安全性,そしてなによりも人的費用,特に参加者である子ども・児童・生徒らの機会費用などを考慮すると,従来どおりの,多数の小規模研究は,費用対効果の観点から徐々に控えられる動きになっていくと思います。私は,当該分野の研究は,純粋に数だけを追うと減っていく,つまりスローダウンしていく傾向を予測しています。
たとえば,悪意のある極端な例ですが,ある教師が自分の職場における役職などの待遇向上だけを動機とする実践研究は,おそらく重要なエビデンスにはならず,そのために研究倫理的に,つまり,そうした倫理面での負の側面と費用対効果を勘案すると,問題のある研究だとみなされるかもしれません。同様に,個人の学位のためだけに,従来教室実験といわれるような実験計画をどう評価するかも難しいと思います。そうであれば,ある程度エビデンスとしての費用対効果が見込まれる,そして倫理審査委員会を通すことができる組織的な大規模研究の方にインセンティブが働くと思っています。
もちろん,エビデンスを巡る議論は,基本的に科学リテラシーや科学コミュニケーションの問題でもあります。そうすると研究マインドというか,研究に関心をもつことは,萎縮どころか,むしろエンパワーメントが重要だと思います。この点を考えると,今後,アウトリーチ活動の重要性が増すと思います。これは「つたえる」「つかう」という点にも関わります。
③多様性や自由を奪う話ばっかり!
さらに基本的にエビデンスを「つくる」ための更に具体的な方策として,本書やその後の関連プロジェクトでは,以下の3つを紹介しています。この点に関連し,著者陣の一部は以下のような学会発表もしました。
- 寺沢拓敬・草薙邦広(2021)「エビデンスに基づく小学校英語に関する基礎概念の整理」第21回小学校英語教育学会関東・埼玉大会. オンライン開催.
- 草薙邦広・寺沢拓敬・酒井英樹(2021)「学会はエビデンスに基づく教育にどのように取り組むべきか?」第21回小学校英語教育学会関東・埼玉大会. オンライン開催.
処遇のプロトコル化・パッケージ化
処遇,たとえば多読だとかタスクだといっても,そこに括られていて,さらに共有されないさまざま手順の違い,そして集団の特性を含むあらゆる条件において結果は変動します。この変動部分を減らすために実験計画法における原則でもある反復と均質化を考えれば,医学分野で行われているようなプロトコル化(手続きや条件の厳正な文書化とその共有,遵守)は十分有効だと考えられます。複数の研究における個々の処遇を同一のものであると認証する厳格な基準が必要なわけです。私はこれを処遇認定手続きと呼んでいます。
また,同時にプロトコルとアウトカムをセットにする行為も有効なはずです。つまり処遇とアウトカムをパッケージ化します。当たり前ですが「処遇AがアウトカムBに及ぼす影響の大きさ」は「処遇AがアウトカムCに及ぼす影響の大きさ」と比較もできません。ある程度,エビデンスを論じるための土台として,処遇―アウトカム関係を固定化する枠組みが必要になります。
アウトカムの規格化・標準化
さらに,アウトカムが氾濫して不一致である状況を防ぐために(そして現状はそういう状況だと認識していますが),社会において合意性を担保できる,つまり標準的なアウトカムを作ります。もちろん完璧なアウトカムとなるテストなどは永遠にありえませんが,少なくとも合意は取れるものを当座的に定める必要があります。これを共通成果とかモデル上の変数となるという意味で,共通成果変数とか共通成果指標と呼びます。正直,成果指標だとKPIのように強烈な管理主義を思わせるので,敢えて私は共通成果変数という聞き慣れない用語を使っています。
このような手続きは一般に標準化,規格化などと呼ばれます。
厳正な因果推論
ここでは詳細は紹介しませんが,もちろん,RCTや事後的に交絡変数の影響を除去する統計分析(e.g., 傾向スコア)が望ましいです。
これらをまとめと,以下の3点が要点です。
- 処遇→マニュアル通りに全部揃える
- アウトカム→定められているものを使う
- 因果推論→多くの研究者には極めて困難
このような方策を紹介すると,エビデンスを「つくる」のに関して,研究者の自由度はほとんど残っていないように思えます。処遇は自分で独自のものを行わずマニュアルに従う,アウトカムは自分で作らず出回っている標準規格を使い,因果推論はある程度高度なので専門家任せ…。これだと研究が萎縮するというのも感情的に十分うなずけます。そこで,結論として「エビデンスは研究者の自由を奪う」という話につながるわけです。もちろん,非常に多いコメントです。
私は以下のように考えます。強いことばでいえば,重要な認識として,エビデンスという観点に限定すれば「逆にその自由こそが問題だった」のです。最初に,処遇について言えば,ほとんどの場合,十分なドキュメンテーションがされていません。実践研究では何を書くべきか,最低限の決まりも明確ではありません。「授業に関する論文では,そもそも紙幅の限界によって記述が十分でない」というのもずっと昔から言われています。私もそのとおりだと思います。
次に,アウトカムですが,英語教育研究者のほとんどが言語テストや心理測定の訓練を受けていません。「素人が思いつきで自作のものさしを使っている」というのもこの分野の自己批判として根強いです。もちろん,問題はそのような品質の自作のものさしでは,効果がそもそも比較不可能だということです。
最後に因果推論についてです。この本の共著者である寺沢さんの発言として,「t検定はエビデンスにならない」などという非常に表面的な彼の言葉尻だけを捉えた話が批判的に話題になる場面を何度か見ていますが,彼はt検定自体を問題にしているのではなくて,交絡変数とサンプリングに関する無頓着さ,つまり因果推論に関する理解の低さについて言及しています。私自身も「検定したからエビデンス!」という話に何度か首を傾げたかわかりません。つまり,それほどこれまでの研究は,因果推論の適格性に疎かったのです。未だに,統計的有意差=エビデンスだという誤った認識が蔓延しています。
まとめると,上記の2つ,つまり処遇とアウトカムはまったく研究者の自由(見たいものを見れて,好きな処遇をやれる)であり,加えて,同時に検定さえすればエビデンスという(誤解に基く)一連の構図が悪かったのです。処遇とアウトカムの自由な導出+無批判的な検定という組み合わせがエビデンスの文脈では問題なのです。どちらかというと,エビデンスに大事なのは,ここの処遇→アウトカムの厳密な因果推論であって,もちろん検定の有無ではありませんし,処遇とアウトカムに対する社会の合意なのです。
このような枠組みでの自由というのが,なんというか,本来,一種の人権論のような規範や価値としてのあるべき自由ではなく,私には単に方法論上の放置というか未着手なのだと思っています。再び,強固な態度だと思われるでしょうが,まずは(心理学のように)手続き的に尺度作成,テスト開発,そして(わたしたちのドメインの仕事として)厳正な処遇の類型,プロトコル化,厚い記述をした上で研究を実施するのがあるべき姿だと思います。これらをしないこと=自由だとはまったく思いません。適当なままでいる自由といったものを認める論には立てません。
また,これもよく質問をいただきますが,私は,エビデンスを議論する際の処遇やアウトカムは,教育現場のレベルから教育行政のレベルまで一貫性を保つ必要があると思います。たとえば,英語教育のアウトカムとして,行政上の資質・能力の3つの柱に十分な関連性をもたせることは,関連分野の1つである心理学や第二言語習得が自由に導出した構成概念よりも,たとえ後者がより学術的に洗練されたものであっても,エビデンスという議論の中では有益だと考えています。
もちろん,公共的でない,または英語教育のエビデンスに関わらない研究,たとえば基礎研究であればまったくこの批判は当たりません。本書にも繰り返し書いたように,基礎研究の立ち位置自体を批判するわけでもありません。むしろ有益な連携と協同を期待するだけです。
…さて主要なコメントについて考えたことを書いたら随分と長くなってしまいました。…前に書いていた「サドコマ」というシリーズネタもそろそろ再開したいと思いますけど,奇特な読者の方,再開しなかったら…そういうことです。
【サドコマ④】有意差がなかったのに効果量が大きい?【効果量の誤解】

英語教育研究の査読で困った!サドコマシリーズ第4弾!とてもご好評いただいております!シェアしてくださると嬉しいです!!
このシリーズについては↓
kusanagi.hatenablog.jp
第4弾では,英語教育研究における「効果量(effect size)に関わる誤解」についての私見を述べます。国内の英語教育研究では,2010年頃から効果量を報告する論文が徐々に増加しました。しかし,それに伴って効果量について根本的な誤解をもったまま研究を進める例が目立つようになりました。そのもっとも典型的な例は,「検定結果は有意ではなかったが,効果量が大を示した。このことから,実質科学的にこの指導法の効果はあったものと考えられる」といった主張です。この主張のどのような点が問題になるのでしょうか?そして英語教育研究において,効果量の報告にはどのような意義があるのでしょうか?
*あくまでもこの記事は英語教育研究を前提にした草薙の私見であり,他分野,または統計学全般の規範とは異なる場合があります。
結論を先にいうと,私が提案する方針は,「検定が有意であったときのみ,効果量へ言及する」と「効果量を使った探索的な研究を推奨する」です。
問題の所在
誤解の始まり
効果量は,記述統計や検定統計量などの組合わせから計算される統計的指標の種類です。効果量と呼ばれる総称的なカテゴリーがあって,その中に具体的に,Cohen's d,Glass's ⊿,r,...といった無数の指標があります。効果量に属す種々の統計的指標は,計算の方式によって,d族の効果量やr族の効果量,または,単純効果量と標準化効果量というようなサブカテゴリーに分けられます。分け方にも複数あって,標本効果量と,不偏推定量としての効果量にも分けることもあります。さらに,効果量に属する多数の指標は,ある組み合わせにおいて換算可能であったり,または換算不可能であったりします。
さて,本来数式で定義されるものを,数式以外の方法,たとえば自然言語で表すと大抵の場合は失敗します。効果量もまさにそうだったと思います。効果量はあくまでも上記のような指標のことですが,しばしば「実質科学的に効果がある度合いを表している」と評されるときがあります。
もともとの目的
「実質科学的な」という表現の含意は概ね,「理論的にp値と独立していること」という点と「相互に比較可能であること」という点だと私は思っています。
たとえば,もっともシンプルな効果量であり,そして単純効果量とも呼ばれる平均差は,その名の通り,2群の平均値の差で表されます。A群の平均値が50,B群の平均値が60だったら,平均差は10です。この値自体は,少なくとも理論的にはp値と独立です。というのも,p値の計算過程の途中に平均差は現れますが,平均差の計算にp値は現れません。
実際の研究ではもちろん,平均差(または効果量全般)の値が大きい場合には,p値が小さくなる傾向にありますが,平均差が厳密に0ピッタリでもなければ,たとえば平均差が0.00001であっても,標本サイズが十分に大きければ検定結果は有意になりえます。
効果量という枠組み自体は「どのような小さい値であれ,検定が有意差を見出してしまうこと」を問題意識としているわけです。見方を変えていえば,「検定が有意であることが,その知見がもつ帰結の重大さを意味しない」ともいえます。よって,効果量には検定後のチェック機能としての役割が期待されます。検定が有意であったときに,「意味のない差ではないか」というように事後的にチェックするわけです。
さらにここから発展して,効果量は研究デザインにおいて中心的な役割をもつようになります。より具体的に,標本サイズの決定に重要です。しつこいですが,検定はたとえ途方もなく小さい差であっても標本サイズが十分に大きければ有意差を検出します。逆に,たとえ大きな差であっても,標本サイズが十分でなければ検定は非有意になります。ですから,研究の事前に効果量の値に目安を立てて,その効果量の検出に十分な標本サイズを設定する必要があります。これは,検定力分析(power analysis)と呼ばれる分析の1つです。「10点の差があったら効果があったといえるだろう。なら,10点の差を見出すために適切な標本サイズを決めよう」といった手続きが典型です。
3つ目,「相互に比較可能であること」とは,たとえば同じ指導法についての研究で,ある研究では10点満点のテストを使用したとして,別の研究では1,000点満点のテストを使用したとします。このとき,2つの研究の平均差を比較しようとしても,スケールが異なるために単純な比較ができません。これを比較可能にするために,それぞれの研究における変数の標準偏差で割ってスケールを揃えます。このようにして標準化平均差といった指標が使用されます。メタ分析は,このような標準化された効果量を使って複数の研究の成果を統合します。
ここまでをまとめると,「実質科学的」といったことばに期待された効果量の機能・目的は3つです。これらはもちろん,数式上の性質によります。この性質を無視して,「実質科学的」ということばの表面だけに着目すると間違った利用が始まってしまいます。
- 検定後のチェック(e.g., 帰結が些細なことを発見してはいないか)
- 研究のデザイン(e.g., 必要な標本サイズの見積もり)
- 比較可能化(e.g., 他研究と結果を比較・統合できるか)
間違った利用
間違った利用方法の代表は,検定の互換・代用として利用される場合です。
効果量には,悪くいえば「文脈を完全に無視した」「恣意的な」,よくいえば,「よく知られている」「慣習的な」基準があって,値を大(0.8くらい?)・中(0.5くらい?)・小(0.2くらい?)といった形容詞に対応させることがあります。このような形容詞の使用の是非は後回しにして,ここでは,仮に効果量が「大」である場合・ない場合と,検定結果が有意である場合・ない場合があると考えましょう。そしてそれらを組み合わせて,以下の4つの場合を考えてみましょう。

タイトルにもあるように,「有意ではなかったが,効果量が大きい」として,研究仮説を支持する事例です。ここで,検定が非有意であり,かつ効果量が大だったときに,対立仮説を支持すれば,これは研究全体としての第一種の過誤の確率を高めます。もちろん,厳密な意味では第一種の過誤ではないのですが,議論を間違ったほうに引っ張ります。つまり,非有意なのに,さも有意であったかのように扱っています。
私は,これを個人的に自己救済措置と呼んでいます。「検定は有意じゃなかったけど,効果量で救済された!私の研究仮説が復活した!」といった例です。自己救済措置は英語教育研究においてとても頻繁に見られます。*1

私はこれを悪意がある行為というよりは,「実質科学的」ということばに惑わされた帰結だと思っているんです。「検定はうさんくさいらしい。でも効果量は実質科学的らしい」と聞けば,応用分野に属する一般的な統計ユーザーは,効果量が真実(実質科学的)を表していて,検定はあくまでも付随的(実質科学的でない)なものだと考えてしまいます。つまり,標本サイズを十分に大きくできないような教育の分野では,「仕方なく有意差は得られなかったけど,本当は効果があるんだ!」と考えてしまうのです。もちろん,感情的にはとても共感できます。しかし,それを差し引いても,自己救済措置はあまりにも危険です。
危険性はどんどん増していきます。たとえば,効果量は小・中・大のどの程度であっても,0付近でもない限りにおいて研究仮説自体を主張するとしたらどうでしょうか。また0.20以下は小だともいえないとしても,0.19999...ならどうでしょうか?結局のところ,研究仮説通りの主張を行う確率が際限なく上がっていきます。

これに加えて,前回の多重検定の記事を思い出してください。こんなグラフを見たことはありませんか?検定の多重性を回避しようとして効果量を報告しているのでしょうが,結局有意でないものの中からいくつか救済して,それらについて,さも有意であったときと同じように扱おうとしているのかもしれません。このような論理展開はあまりにも危険です。

端的に効果量の誤差を無視していることが危険性の根本にあります。たとえば,実際には効果量が0だとしたとき(母効果量を0だとする),毎回標本を得れば,その度に効果量の値(標本効果量)は0を中心にばらつきます。そして,標本が小さければ小さいほど,そのばらつきは大きくなっていきます。
少し複雑に思われるかもしれませんが,こう考えましょう。本当の効果量が0のときに,標本効果量が,ある特定の値以上を取る確率を大きくする一番簡単な方法は,標本サイズを下げることです。標本サイズが小さいと誤差が大きくなりますから,その誤差によって大きな効果量が得られる確率は上がります。これでは,誤差が大きくなることを期待して,小標本の研究を行うことにインセンティブが働いてしまいます。
こんなシミュレーションをしてみましょう。各群の標本サイズにおいて,100,20,8人の3パターンがあるとします。母効果量を0だとして,それぞれ1,000セットのデータを生成し,その全てのセットにおいて効果量(d)をもとめます。本当は効果がないことのメタ分析を行っているイメージですね。そのシミュレーション結果が下の図です。8人の場合なら,たとえば0.20より大きくなったのは,全体の約35%です。実際に効果量がないというシミュレーション上の環境ですら,8人の比較だと,35%くらいの確率でポジティブな方に効果量を示します。そして第一種の確率が(片側の)2.5%だとすると,シミュレーション結果のうちの33%は「有意じゃなかったけど,効果量はすくなくとも小程度あった」というパターンになります。ちなみに中以上(0.5以上)だと約15%がそのパターンになります。

結局,人数が少ない実験をすればするほど,「有意じゃなかったけど,効果量はあった」という議論がしやすくなります。
同じように,検定の互換として「効果があるか?」とRQにおいて問い,効果量の任意の値をもって効果があると結論づけるのも場合によっては問題です。上記のように誤差を考慮していないからです。
さらに,ここまでの話とまったく同様に,有意傾向というのも,ただの非有意のことなので用いるべきではない言葉です。
原則
原則は,もちろん,「有意差が得られなかったときに,標本効果量を証拠として研究仮説を主張しない」です。このような展開は絶対阻止です。査読でこのような論文が見かけたら,最初にこの点を徹底的に改める必要があります。これを正当化することはできません。
しかし,これにとどまらず,効果量の本来の目的に忠実に沿った使用を心がける必要があります。英語教育研究に関する状況を考慮して,英語教育研究に限り,私は以下の3つの方針を具体的に提案します。
- 検定が有意であったときに限り,効果量の値に言及できる
- 効果量の値への言及は,根拠とともに示す。根拠がないなら言及しない
- 探索的な研究における効果量の報告を推奨する
妥協案の提案
検定が有意である場合のみ言及
効果量の1つ目の健全な使い方は,前で述べたように事後的チェックです。事後的チェックというよりも,結果に対する反論への予防線と考えた方がいいでしょう。そもそも,統計的帰無仮説検定という仕組み自体が,学術コミュニケーションにおける機能に着目すれば,結果に対する反論への予防線です。
たとえば,有意であることが,機能的に何を意味するかというと,「それは偶然ではないか?」というタイプの反論に対するカウンターエビデンスです。検定が有意であれば,「偶然ではなさそうだ」ということの証拠の1つになります。同様に,「有意差があったが,実際には意味がない値ではないか?」という反論があったとしたら,効果量の報告は「意味がないわけではなさそうだ」という種のカウンターエビデンスになります。反論があるから,それを予防しているわけです。
このことを考えれば,そもそも検定が非有意であるとき,偶然ではなさそうだとも返すこともできないので,次の予防線を張る意味がありません。つまり,「偶然かもしれないが,意味がありそうだ」という種の主張にはまったく説得力がないでしょう?ですので,検定が有意じゃなかった場合には,そもそも効果量の値について積極的に言及する必要はないと思います。
なぜ,あえて言及すらしないかというと,有意じゃないときに効果量の値に言及すると,いずれにせよレトリックを使って対立仮説を支持するような議論になる場合が多いからです。あえてそのような展開を防ぐためにも,危ない橋は渡らないということです。
効果量への言及は根拠を示す
次に,上記の事後的チェックとして効果量へ言及するときは,いわゆる大・中・小基準以外の根拠をもって言及すべきだと考えます。少なくとも理想的には,です。
より具体的にいえば,大・中・小といった表現自体は使用しない方がよいと思います。大・中・小とは,一般に検定力分析を行う際などの目安であって,統計的な計算上の通例だけに意味をもっています。より具体的な,特定の文脈,たとえば,「ある実験条件があるアウトカムに及ぼす影響」とか「ある処遇があるアウトカムに及ぼす影響」といった文脈をもつ場合において使用すべきではありません。つまり,ある具体的な研究において,「効果量が大であった」とか「小であった」という表現は英語教育研究では基本的に不必要だと思います。
効果量の値は,あくまでも特定の文脈をもつ場合に限定して,その文脈内における相対的な比較のみに役立つと考えたほうがよいかもしれません。たとえば,「ほぼ同条件で行った先行研究の実験と同等の効果量だ」といった具体的な事例を引用した上で言及するべきかと思います。
探索的な研究における効果量
研究仮説が特にない探索的な,または記述的な研究において,効果量を報告する必要がないかといえばそうではありません。
むしろ効果量の役割として,将来行われる研究のデザインに貢献することができます。たとえば,探索的な目的の下で,検定をせずに記述統計と効果量を報告する研究があったとします。この研究では確かに強い主張をすることはできませんが,少なくとも仮説形成には役立つはずです。そして仮説形成だけでなく,次の検証的な研究のデザインを可能にします。たとえば,この論文で,標本効果量d = 0.40を示したとします。この探索的な効果量の報告から検定力分析を行って,各群の標本サイズがおよそ100人ずつ必要なことがわかります。次の検証的な研究では100人ずつの実験を行うとよい,といった具合です。
さらに,探索的な研究であって検定を行っていないとしても,効果量が報告されてあれば,将来的にメタ分析で参照される可能性もあります。 もちろん,APAなどでは効果量の報告を求めています。
このように,研究は競争的な側面もありますが,基本は科学コミュニティ全体のチームプレイです。チームプレイにおいてこのようなバトンの渡し方はもっとも理想的なものです。このシリーズでは何回も繰り返しますが,英語教育研究において,1論文の価値はそれほど高くないものです。だからこそ,英語教育研究全体が協同的に,効率的に作業を進めていけるような仕組みが必要だと思うんです。そして効果量はそのような仕組みの足場の1つだと思っています。効果量は有意じゃないときの救済措置ではなくて,複数の研究をつなぐバトンだと思いましょう。
考えておきたいこと
さて,特に教育実践を視野に置くと,効果量に属する指標だけが特別重要だというわけではありません。確かに効果量は研究デザインなどにおいてとても重要ですが,「大きい効果量を示した指導法がよい」といったことばかりに囚われるべきではないかと思います。効果に限らず,リスクやコストなどについての観点も重要です。
国内の英語教育研究の例を挙げると,寺沢(2018)*2は効果量に対する言及の仕方を示す手本の1つになるかと思います。この論文では,約3,000人の調査データを使用し,構造方程式モデリングを行っています。目標としては,小学校における英語経験が英語学習への態度,英語のスキル,そして異文化理解といったアウトカムに及ぼす効果を推定することです。寺沢は,まず,上記のようなアウトカムに対する効果が有意であることを報告しています。しかし,その後,以下のように論じています。
第一に、前述の通り、本研究で示された小学校英語の効果は(たとえ統計的に有意だったとしても)ごく微弱なものであり、政策導入に必要なコストに見合うものかどうか疑問を抱かせるものである。もっとも、本分析で示された効果量自体は――たとえば偏差値 1-2 程度の向上は――、介入に要するコスト次第では有効性と見なせることがある。たとえば、千円程度の小冊子(たとえば副読本やドリルブックなど)を配布するというコストの小さい教育的介入で、これだけの成果が上がるのであれば大いに評価できるだろう。
しかしながら、小学校英語のコストはこの対極にある。多くの論者が指摘しているとおり、小学校英語を施行するには教員の再研修、教員の配置、教材・カリキュラムの整備などに莫大なコストを要する (Hashimoto, 2011; 藤原・仲・寺沢, 2017)。これだけのコストに対して、偏差値にして 1-2 ポイントほどの上昇を、小学校英語の有効性と解釈するのは困難と思われる。(寺沢, 2018)
まさに,検定後の事後チェックとして効果量に言及しており,効果が「あるかないか」といった二極思考ではなく,効果の程度自体に着目し,さらにそのコストを割り引いた上で効果量について議論しています。丁寧に標準化係数を偏差値換算し,そしてコストにかかる証拠となる文献を挙げています。そして「疑問を抱かせる」といったように断定的でない表現を使っています。規範的です。
大事なことは,統計的な意味での効果,そして効果量自体は,私たちの複雑な意思決定における要因の1つでしかないということです。私たちはそれ以外にもコストやリスクについても考えますし,そしてそもそも定量化できないことにすら価値を見出すでしょう。最初の話題に戻りますが,そしてしつこいですが,効果量はある種の統計指標のカテゴリーの名前です。効果量を使うとき,いつもそのことを思い出すべきだと思います。効果量で目を曇らせてはなりません。
最後に,効果量の信頼区間の報告も重要です。なかなか査読などで求めることは少ないかもしれませんが,効果量は信頼区間と合わせて報告すべきです。ただ,シリーズ第1弾で述べたようにそれが難しいのなら,生データを公開するほうが便利だと思います。同じように,効果量にもたくさんの種類があります。これらの氾濫もまた問題とされており,換算性の高い共通言語効果量というのも考案されています。「効果量のどれを報告すればよいか」という問題もありますが,まずは生データ自体を公開するように努めるほうがよいかもしれませんね。
サドコマシリーズ10箇条
…さて,と!これで新しいあいことばが増えました!
- 報告不備には生データ
- null resultsも評価する
- 検定の多重性は研究仮説を見る
- 有意じゃないとき効果量には言及しない
次回は事後分析について書きます!今回は軽めでしたが,次回は重めの自信作です。
私はSNSなどをやっておりませんので,どんどんシェアしていただくと幸いです!広くいろんな方に読んでいただけるよう一生懸命書いてます!
【サドコマ③】検定めっちゃ繰り返してる…【検定の多重性】

英語教育研究の査読で困った!サドコマシリーズ第三弾!とてもご好評いただいております!シェアしてくださると嬉しいです!
このシリーズについては↓
kusanagi.hatenablog.jp
こんにちは,草薙です!第3弾では,英語教育研究において頻繁に見られる「検定を多数繰り返している論文」(多重検定論文)についての私見を述べます。はっきり言って,この問題は深刻です。英語教育研究の発展を妨げるもののランキングがあったら,漏れなく5位には入るでしょう。そのため,今回の記事は特に長いです。なにせ,このシリーズの中で一番気合を入れて書いてますから。
さて,統計的帰無仮説検定において,検定の繰り返しはよくないこととして広く知られています。英語教育研究においても,1990年代後半から現在に至るまで,検定の多重性の問題は一部の研究者によって繰り返し指摘されてきました。しかし,2020年においても検定の多重性が見られる論文は少なくありません。この記事では,英語教育研究における多重検定論文をどのように改善するかについて述べます。
*あくまでもこの記事は英語教育研究を前提にした草薙の私見であり,他分野,または統計学全般の規範とは異なる場合があります。
結論を先にいうと,私が提案する方針は3つです。
- 検定の多重性に関わらない研究仮説を立てる(検証的な,論理積の研究仮説)
- 検定の多重性に関わる場合は統計を行わない(探索的な,論理和の研究仮説)
- どうしても多重比較を行う場合はボンフェロー二の補正を使うべき
問題の所在
そもそも検定の多重性って?
検定の多重性はよくないこととして知られているものの,曖昧な理解に留まっている方も多いです。最初に,この問題について解説します。
たとえば,それぞれに異なる処遇を与えたA群,B群,C群とがあり,成果変数(outcome)における各群間の平均差について知りたいとします。有意水準α = .05をもって,それぞれA群-B群,A-C群,B群-C群についてt検定を3回繰り返して適用するとします。仮にA群-B群,A群-C群,B群-C群の平均値がすべて等しい場合,3つ行った検定のうち,どれか1つが誤って有意になる確率(第一種の過誤,この場合は特にFWER=familywise error rateといいます)*1が,もともとの有意水準(公称の有意水準)よりも高くなります。
つまり,「本当はどこにも差がないときに,誤ってどこかの群間に差を見出してしまう確率が検定の繰り返しに伴って高くなってしまう」という問題です。この関係はシンプルです。第一種の過誤の確率が,仮にn個の検定なら,となります。たとえば,検定数が3個の場合におよそ14%です。

複数の群を総当りで比較する場合,とんでもないことになります。8群総当りの比較では,ですから,
を計算すると,76%にもなります。参考に,群数と第一種の過誤の関係も可視化しておきます。数式としては,群数がm個のとき,第一種の過誤の確率は,
になります。ここでのαは.05です。

これは群間の比較に限りません。たとえば永田・吉田(1997)*2は,検定の多重性の問題は,(a)多項目,(b)多時点,(c)検定の種類,(d)サブグループ,そしてこれらの組み合わせといった場面においても発生するとしています。
日本の英語教育研究における典型的な例は以下のようなものです。
- 20個の質問項目すべてにおいて,被験者の学年(1年,2年,3年)間の多重比較を行った(検定数は60ですから計算上第一種の過誤は計算上およそ95%)
- 全10回の授業回それぞれにおいて,3群の多重比較を行った
- 8群の平均値に対して,t検定およびU検定をそれぞれ行った
英語教育では,水本(2009)*3が多項目(多重エンドポイント)で検定を繰り返す例について指摘しています。質問紙の項目全部を検定するといった場合が多重エンドポイントによる検定の多重性です。同様に,草薙・田村(2017)*4は特にサブグループ解析について検定を繰り返す例を取り上げています。点数で上・中・下群に分けて差を事後的に検定するといった場合がサブグループ解析です。
よりカジュアルなこの問題の記述としては,この記事をご覧ください。
第一種の過誤の増加よりも目的の履き違え
ところで,たとえば,医薬分野について考えましょう。この分野では,効果がない治療法や新薬に対して誤って効果を見出してしまっては危険です。たとえばコロナウィルス感染症の治療薬として,効果がない新薬を認可したら大変です。副作用もあるかもしれません。同時に,このような効果検証の手続きに,時間的な制約がある場合もあります。たとえば,コロナウィルス感染症の対処療法の確立はできるだけ早く社会から望まれます。時間や予算の制約から,複数の療法や薬を,複数のエンドポイント(たとえば,咳,熱,倦怠感など)で同時に比較しなければならないときもあります。医薬分野においては,このような事情によって多重検定に伴うFWERを制御するための議論が徹底して行われます。
しかし,英語教育研究はこの分野とは文脈が異なります。英語教育研究では,「ある指導法に効果がある」と論文に掲載されても,素早く教育現場に浸透することはありません。同時に,余程の拙速な政策施行や制度改革がないなら,英語教育研究者が効果検証を急ぐ必要もありません。なので,私は,正直にいうと,FWERの制御技術云々は英語教育においては比較的重要なことではないと思っています。というよりも,さらに悪いことがこの問題の中に潜んでいるからです。
それは,意思決定的(decision-making)で,検証的(confirmative)な方法である統計的帰無仮説検定を,仮説形成的(hypothesis-formulating)で,探索的(explorative)な方法のように使用することです。そもそも,統計的帰無仮説検定の設計思想は,十分に統制された実験的状況下において,比較的小標本のデータを使って,ある具体的な仮説を検証するというものでした。雑多なデータの集まりから,研究者が予想しないパターンを網羅的に,そして自動的に抽出する方法ではありません。後者は統計的帰無仮説検定というより,一般にデータマイニングといわれる分野の領域です。
私は英語教育研究において,仮説形成的で探索的な試みをとても重要視しています。研究はすべて検証的でなければならないとも思いません。第一,私自身が専門とする数理モデリングはかなり探索的ですし,質的研究や記述的研究も正当に評価されるべきだと思います。ここで批判したいのは,その探索的な研究目的ではなく,方法の選び方です。
繰り返しますが,統計的帰無仮説検定,特に多重比較は効果のデータマイニング装置(草薙・田村, 2017)ではありません。「よくわからないけど取れるだけのデータを取って,全部多重比較に突っ込んだら科学的な真実が自動的に明らかになる」といった便利なツールではないのです。統計は,なんでもデータを突っ込めば科学的真偽を判定してくれる道具ではありません。研究者が,自然を観察し,観察から仮説を作り,そしてその仮説を検証する方法です。観察→仮説形成→検証というステップにおいて,統計的帰無仮説検定が検証を担っています。観察や仮説形成は統計的帰無仮説検定の主たる役割ではありません。
私は,誤った目的での統計的帰無仮説検定の使用を,英語教育研究から追放する必要があると考えてます。つまり,「第一種の過誤の確率を減らす」という技術的問題よりも遥かに前のレベルについて私は述べているのであり,実際にありとあらゆるQRP(Questionable Research Practice; 疑問符がつく研究実践),特にHARKingに密接に関連していることが悪いのです。
なぜこうなってしまったのか
現在私は,このような研究実践自体を,研究者の無知や悪徳というよりは,むしろ歴史的な,社会学的な,そして経済学的な分析対象だとして捉えています。つまり,このような研究実践が生まれる必然的な背景があったと考えます。以下に考えられるいくつかの要因を書きます。
- 英語教育研究者の養成過程において,統計分析等に関するカリキュラムが十分に提供されている例は稀であった(特に1990年代~2000年代)
- 1990年代以降,統計分析を行うコンピュータ・ソフトウェアが急速に普及しはじめ,訓練を受けていない研究者が使用できるようになった
- 2000年代,大学院重点化などによってパブリケーション・プレッシャーが高まり,統計を使用しない論文は載らなくなっていった
- 2000年代,指導法効果検証ブームによって,パブリケーション・バイアスが高まり,null resultsの論文は載らなくなっていった
- 教育を研究対象とする限り,標本サイズの統制が困難であり,小標本は必然的にnull resultsに繋がりやすい
- 成果変数(outcome,テストや質問紙など)を比較的自由に開発する文化がある
- 学際的であるがゆえに理論的基盤がないため,そもそも形式化され,焦点が絞られた仮説が成立しづらく,研究全体が概して探索的である
つまり,英語教育研究者は,統計を使用し,有意差を報告しなければならない圧力に慢性的に晒されています。そして理論的足場が弱いために,検証的な仮説が立てられません。加えて,小標本であれば有意差が得られにくいですから,有意差を得るために,テストや質問紙を自作し,同時に取得するデータの種類を増やし,事後的にグループを分けるなど,とにかく検定数を増やさなければなりません。このような状況では,表面的には検証的で,実質的には探索的な方法が好まれることも納得できます。
結局,具体的な仮説を作らずにおき,根こそぎデータ全部をたくさんの検定にかければよいのです。そして検定結果を見てから最後に整合的な仮説を書けば(HARKing),仮説検証的で有意な証拠を示す科学的な実証論文が「いっちょできあがり♪」です。
私は実際にこのような方法が優れた研究規範として伝えられていたり,または指導されている例を何度何度も見てきました。いわく,「仮説は最後に書く」「結果から論文を書き始める」といったノウハウです。
…先に改めるべきは,FWERの増加による結論の誤りというよりは,このresearch traditionです。この手順が恐ろしいのは,仮にこのノウハウを教わっていなくとも,いずれ研究の過程で自然に見につけてしまうことです。つまり,HARKingは,統計の仕組みに詳しい1人の悪質な研究者がそれを発明し,それが闇市場で広く流通しているのではありません。自然に,どの分野でも,いつでも発生し,身につけた研究者が自然に増加していくのです。
実は検証的な場合は問題がない
ところで,英語教育研究の分野では知られていないことですが,複数の検定を行っているからといって,必ず検定の多重性の問題を抱えているとは限りません。ある特定の研究仮説(RQ)をもつ論文では,検定の多重性の問題がなく,有意水準の補正といったFWERの制御自体が不要です。
具体的には,研究仮説が複数の検定結果の組み合わせ,つまり論理積(かつ,and,A∧Bと書きます)のみによって表現できる場合がそうです。たとえば,研究仮説において「平均値の高さがA群 > B群 > C群である」と示される場合では,(A > B)∧(B > C)∧(A > C)といった3つのt検定の対立仮説の論理積によって相当します。ここではそのような研究仮説を,論理積の研究仮説と呼びます(この用語は一般的ではありません。私は重要だと思いますが…)。繰り返しますが,このような研究仮説の場合,検定の多重性は問題ありません。
少し難しいかもしれませんが,以下のように考えましょう。ある成果変数の平均値差について,A群とB群が等しいという帰無仮説をとします。A群とC群が等しいという帰無仮説を
とします。B群とC群が等しいという帰無仮説を
としますこの3つの仮説を組み合わせて,それらの真偽表を考えると,以下のようになります。我ながら親切なことに,合わせてベン図も描きます。

そもそも検定の多重性とは,第一種の過誤,つまり帰無仮説が正しいときに誤って対立仮説を採択する確率のことですから,α = .05で3つの検定を行えば,3つすべてが同時に第一種の過誤である確率は,になります。よって有意水準の調整も必要ありません。
一方,研究仮説が論理和(または,or,∨と書きます)の集まりで構成される場合はどうでしょうか。つまり,「こうかも,またはこうかも,いや,こうかもしれない,いずれにせよ,これらの場合のうち,どれかは正しい」といった種の研究仮説のことです。ここでは論理和の研究仮説と呼ぶことにします。厳密にいえば,排他的論理和というべきです。言葉での説明が長くなりますから,先にイメージを掴むために図表を描きます。

このように,論理和によって,組み合わせの場合全体が研究仮説になっているのですから,誤りの確率が足されていくのです。
英語教育研究においては,研究仮説ではなく,Research Questionとして示されているとき,特にRQに以下のような表現を含む研究は,後者の論理和の研究仮説に分類されることがほとんどです。こう考えると,英語教育研究の大多数が論理和の研究仮説を持っています。
- どのように(how)
- なぜ(why)
- なにが(what)
- いつ(when)
- だれが(who)
- どの面において(in which aspect)
- どの順番で(in what/which order)
お気づきのように,5H1Wの疑問文です。もう少し文脈をつけて具体例をあげますね。
- 統合的動機づけはどのように学習者の自律学習を促すか,または促さないか
- なぜ多読行動において理想的な自己像は重要な役割を果たすのか
- 学習者が授業中に気づきを経験するのはいつか
- どの質問項目がもっとも学習の成否を分けるか
- どのような心理的側面においてシャドーイングはポジティブな効果をもつか
- 文法形態素はどの順番で習得されるか
しつこく繰り返しますが,検定の多重性が問題になる場合は,このような論理和の研究仮説の場合です。
これらの研究は,概して探索的な性質を持ちます。もちろん,研究仮説が明示されていない,または実証結果との対応が取れない研究も同様です。「観察→仮説形成→検証」というステップにおいて,この種のタイプはあくまでも「観察→仮説形成」のステップです。仮説がない「観察→検証」とか,逆方向の「検証→仮説形成」ではありません。
論理積の研究仮説のイメージは,スナイパー式です。ある1つの仮説に狙いを定めて,複数の弾丸を発砲します。1人の両手両足を狙撃して,全部が当たることでやっと敵の動きを封じるイメージです。一方,論理和の研究仮説はショットガン式です。適当な方向に向けて散弾を発砲します。数ある散弾のうち,どれかが何かには当たるだろうというわけです。
原則
さて,この問題に対する私の方針を書きます。
1つ目は,論理積の研究仮説を立てることを推奨するというものです。研究仮説をそのように書けばよいというレトリックの問題ではなく,複数の検定結果のすべてが予想通りだったときのみ,その場合に限って研究仮説が実証されたとみなすような研究仮説を立てて,研究全体をデザインする必要があります。
次に,仮説形成的で探索的な研究,特に論理和によって表される研究仮説をもつ研究は,統計的帰無仮説検定を一切行わないということです。あくまでも「観察→仮説形成」というステップですから,検定を使って多重比較を行うのではなくて,データの記述やパターンの発見に留まるべきです。
最後に,どうしても多重比較を行う必要がある場合は,最も保守的かつ検定統計量の種類や前提に関わりなく,汎用的なボンフェロー二の補正を行う方がよいと考えています。

妥協案の提案
論理積の研究仮説の場合
ここからが具体的な提案です。査読者は,検定の数を見るだけではなくて,むしろその研究の文言をチェックする必要があります。前述の通り,論理積の研究仮説の場合には,余計に有意水準の補正を求める意味はありません。査読段階で仮説を書き直すよう提案することはできませんが,論理積の研究仮説として形式化できる場合は,仮説を明確化することも重要です。
逆に投稿者は,先行研究や理論的背景が十分にあるのならば,論理積の研究仮説を予め定めるようにするとよいでしょう。これが最も大事な方針です。
仮説の作り方のより具体的なテクニックとしては,自然言語の疑問文の形をとるRQや,研究目的(purposes)ではなくて,検定結果に対応する具体的な研究仮説を書くとよいでしょう。つまり結果に関する論理的な命題,宣言,または数式で結果を表現します。RQとして「どの群の成績が一番高いか?」と問うのではなくて,仮説として「A群の平均値はB群の平均値およびC群の平均値よりも高い」と書きます。もちろん,研究スタイルにも多様性がありますから,場合によっては目的,RQ,仮説を併存させても構わないでしょう。一般に「もしも<要因>を<水準>にすると,<アウトカム>は<効果・予測>になる」と書くと,仮説検証のしやすい仮説になります。
ところで,論理積の研究仮説ならば常に問題ないかというと,そうではありません。論理積の研究仮説が尤もらしい(plausible)仮説であるかを査読者は評価すべきです。やたらと無根拠に検証的であったりする決めつけ仮説を,高く評価することはできません。決めつけ仮説は,しばしば,著者の強すぎる信念か,特定の集団の規範や権威に支配されています。
また,決めつけ仮説は,HARKingの産物である可能性が高いです。論理積の研究仮説の場合だから大丈夫とは思わず,決めつけ仮説でないかを入念に査読者が検討する必要があります。同様の理屈として,もともと探索的な研究において,仮説がやけに明確に書いてあると,それはただの決めつけです。研究者の先入観を表してるに過ぎません。そのような場合は,中立的に研究目的やRQを書くべきです。大事なことは,研究目的,RQ,仮説を研究が持つ態度によって適切に使い分けることです。英語教育研究ではこの部分が大分後進的であると感じます。
次に,私が個人的にすり替わり仮説と呼ぶ種の仮説もあります。英語教育研究では,非常に多い例です。正直,溢れかえっています。ARELEとかLETとかLLとかSSLAの掲載論文を網羅的に調べ,当該分野における仮説のすり替え率を発表する研究をするか悩むくらいです。(興味のある人,個人的に連絡ください)
すり替わり仮説は,論理積の研究仮説のように書かれています。たとえば,多重エンドポイントのデザインによって,「多読行動は,読解意欲,単語力,文法力のすべての変数に効果がある」と形式化されているとします。これは確かに,検証的な論理積の研究仮説です。しかし,たとえば,読解意欲の変数のみにおいて平均差が見られなかったときに,つまり結果を知って,結論で「多読行動は,単語力,文法力にのみ効果があることが解明された」と書けば,典型的なすり替わり仮説です。
一見何の問題もないように見えますか? よく「え?何が悪いの?」と聞かれます。しかし,これは問題です。というのも,当初の研究仮説に対して整合的な結論は,「多読行動は,読解意欲,単語力,文法力のすべての変数に効果があるとはいえない」です。これは研究仮説である「多読行動は,読解意欲,単語力,文法力のすべての変数に効果がある」が採択されなかったのだから,null resultsを報告するべきです。このnull resultsとして結論づけるので,有意水準の補正が不要なのです。すり替え仮説のケースでは,最初に特定の仮説を立てておいて,途中で検定結果の組み合わせによってありえるパターンのいずれかにすり替えています。これらの論文は「仮説において考えてもいないことを突然主張し始める論文」なのです。逆にHARKingして美しく見える論文の方が悪質ですが,大抵は先行研究との整合性が怪しいため気づきます。
いずれにせよ,査読者は上記のような研究仮説の吟味を行って,本当に検定の多重性の問題があるかないかを考える必要があります。同時にHARKing,すり替え,または決めつけがないかもチェックします。大事なことは,統計の処理を見るのではなくて,むしろ仮説と結論を見るということです。このシリーズでも繰り返し指摘してきましたが,統計に関する問題点のほとんどは,実は研究仮説と結論にあります。
論理和の研究仮説の場合
多重比較に用いられるボンフェロー二の補正,テューキーの手順,ホルムの手順,ダネットの補正,シェッフェの方法…などなどといった多重比較の諸方法は,本来,論理和の研究仮説の際に使用されるために開発されたものです。ですが,結局のところ,医薬分野とは異なり,研究目的があくまでも仮説形成的で探索的な場合が多い英語教育研究では,そもそも上記のような多重比較ではなくて,その顕著に探索的な目的に即した方法を使用すべきです。最近はラーニングアナリティクスとかエデュケーショナルデータマイニングといった分野もあります。どちらかというと,これらの分野の手法の方が,英語教育の文脈に沿う場合が多いと思います。
たとえば,複数の群間における平均差のパターン抽出だったら,適切な可視化の方が有効です。記述統計を報告し,それを可視化し,そのパターンについて「解明された」であるとか「証明された」であるといった検証的な用語を使用せずに,「C群は他の群よりも相対的に高い平均値の傾向を示した。統計的根拠はないが,この傾向を仮説として次の研究で検証したい」と締めくくる論文の方が,遥かに学術的貢献は大きいです。まさに探索的に観察をして,仮説形成を行っていますね。査読において,このような研究の価値を積極的に認めるべきでしょう。
逆に,論理和の研究仮説を検定にかけることは,多くの方が思うより,ずっとずっと恐ろしいことです。たとえば,「どのように」と問えば,複数の検定結果の組み合わせがどのようになっても「そのように」という結論を導きます。「なぜ」と問えば,複数の検定結果の組み合わせがどのようになっても「こうだから」という結論を導きます。最初に決まった仮説がないのだから,後付で恣意的に解釈できてしまいます。つまりどの場合でも間違いがないように見えるのです。全部の群間がnullでもない限り,null resultsになりません。なにかが解明されます。
チェック機能が働かないことも問題です。後付による恣意的な議論も,確固たる理論体系がなければ反駁できません。さらに前回の記事で述べたように,パブリケーション・バイアスを考えれば,そもそも実証的に否定されにくいのです。これによって誤った後付の,恣意的な解釈が理論化されて私たちの分野に居残り続けます。このようなチェック機能として,英語教育研究には形式的で強い理論や公理や原則が必要なのです。
少し話が逸れますが,英語教育研究における議論や考察(discussion)または解釈を殊更重要視するユニークでローカルな研究規範とも繋がっています。私はこれを後付主義と呼びます。研究計画段階よりも結果が出た後の知的活動を重視するアプローチだと定義します。このアプローチでは,「結果がなぜそうなったか」「結果をどのように解釈するか」「結果から何が主張できるか」が重要視されます。英語教育の学会では,いつも研究熱心な方々がこのように質問されます。私は個人的に「くにちゃんの研究にはサスペンス感がない」と言われたことがあります。
しかし,「結果がなぜそうなったか」と結果を見てから想像の所見を加えるというよりも,結果を事前に予測する仮説の方が重要ではないですか?「結果をどのように解釈するか」というよりも,解釈の仕方が一様に定まる研究をデザインするべきではないですか?「結果から何が主張できるか」なんて,もはや結果と主張の関係性が弱いことを自ら表明しています。主張を明確に支える証拠が重要ではないですか?
このようなアプローチは,結局のところ,仮説形成的で探索的な目的を無理やり検証的な形式に変換した際の齟齬そのものに過ぎません。「なぜそうなったか」は結果を所与のものとして逆に仮説形成しています。「どのように解釈するか」は,解釈の仕方すら探索しています。「何がいえるか」はもはや示唆や結論を探索しています。検証的な研究と探索的な研究の区別が全くついていないのです。サスペンス感とは,結局後からあれこれ場当たり的に論じる展開のことですよね。
…などと「常識的な議論や考察の力量が完全に欠落している」研究者である草薙は申し上げておきます。これは私が査読者さまから頂いた一番のお気に入りフレーズです。でもここに書けてスッキリしました♪
ちょっと感情的になりすぎましたが,論理和の研究仮説がいかに仮説形成的,探索的で,そしてなぜ統計的帰無仮説検定を応用すべきでないことがわかっていただけるかと思います。もちろん,先に書いたように私は探索的な立場,特にアブダクションの機能を重要視しています。それを履き違えることを強く批判しているのです。
どうしても多重比較を行う場合
さて,どうしても論理和の研究仮説を立てて,多重比較をしなければならない場合もあるかもしれません。そのような場合は,もちろん適切な手続きを取るべきです。
最初に,特に多重エンドポイントの場合に考えるべきことは,変数の集約です。たとえば質問項目が複数あれば,そこから合計得点を使用したり,合成得点を作ったり,または因子分析などを行って因子得点にするなどして,とにかく変数の数を減らすべきです。
次に,それでも変数の数が1つにならないときは,変数の優先度を宣言します。「この変数は本研究の主要な変数だ」とか「この変数はあくまでも補助的な参考である」といった具合です。レベルやランキングをつけても構いません。基本的に,補助的な変数まで全部多重比較する必要はないかもしれませんし,このように優先度を考えると検定数自体を減らせることもできます。
3つ目に,本当に必要な検定だけを絞り込みます。たとえばCを統制群として,AとBの両方を別の処置群だとする場合,AとBの間の検定は必要ないかもしれません。この場合,AとBの間については検定しなくても構いません。必ずしも総当りで検定しなくてもいいわけです。また,たとえば3群の平均値の比較において,1元配置の分散分析を実施し,これが有意だった場合のみ,それぞれの群間のt検定を行うという分析法(下位分析)が慣習的です。この分析はそもそも多重比較において,閉手順などといって,検定数をできるだけ減らすためのフレームワークに由来します。重要な分析手順ですが,研究仮説によっては,最初の分散分析が不要な場合もあります。たとえば,「研究仮説がA群,B群,C群のうち,どれが高いか」といった仮説であれば,最初の分散分析を飛ばして,t検定を3つ行えばよいと思います。分散分析の帰無仮説はこの仮説と整合的でないからです。
さらに,検定のための検定(e.g., 等分散性のための検定や正規性の検定)も厳密に言えば帰無仮説族を形成します。つまり,(正規性がある)∧(等分散性がある)∧(2群に差がある)といった場合です。これらの場合は,できるだけ検定のための検定を避けて,代替的な方法を取る方が無難です。より統計上の前提条件のゆるいロバストな方法を使うとよいでしょう。
さて,最後が,ようやく多重比較の実施です。多重比較の方法はそれこそ無数にあります。場合に応じて,さまざまな方法を選ぶことができます。しかしその選択こそが難しいのです。群間,従属変数,または時期など,それらの組み合わせによって方法は全く異なりますし,等分散性や正規性といった統計的条件によっても異なります。さらに,ある種の党派性や手法の哲学争いがあります。たとえば,教育心理学では,A大は伝統的にホルムで,B大はテューキーで,C大はステップダウン・ボンフェローニで…といった話を聞いたことがあります。結局,これらの方法の選択はかなり技術的で複雑なため,英語教育研究ではこれらの方法のどれがよいかについて吟味する必要はそれほどないと考えます。
よって,私は,英語教育研究の一般的な研究に限り,ボンフェロー二の補正を推奨します。シンプルに有意水準αを検定の総数Nで割るというもの,つまりN個の検定を行う場合を有意水準として検定するわけです。もっとも有名,かつシンプルです。学習費用およびコミュニケーション費用が最安でもあります。そして,どのような統計量であっても同じように計算でき,統計的解析環境やソフトウェアに限らず実行でき,何よりも最も保守的です。保守的であるとは,もっとも有意差が出にくいことです。あまりにも保守的であるという理由で,その他の方法が好まれますが,それでも,英語教育研究のほとんどの場合では,ボンフェロー二の補正が適切だと思います。もちろん理由もあります。
1つ目の理由です。保守的であるということは,同時に第二種の過誤,つまり有意差があっても見逃す確率も高まること(検出力が低い)を意味しますが,英語教育研究の文脈では,第二種の過誤が深刻な問題になる場合は少ないと予想されます。現実世界において,第一種の過誤の方が遥かに深刻です。その第一種の過誤ですら,教育上の応用との断絶を考えると,それほど問題でないと考えられるレベルです。
2つ目は,少し帰結主義的ですが,この保守性,検出力の低さには,悪質な研究仮説を抑制する効果があると期待するからです。仮に研究者が強く有意性を求めるのであれば,「ボンフェロー二は有意にならないからそもそも多重比較はやめよう」となるのではないかと思います。
3つ目です。実は,英語教育研究における過去の論文を見ると,平均的に報告される効果量は小さくありません。そもそも対象とする現象の効果量が大きい場合が多いのなら,検出力の程度に拘泥して,技術的に高度化させる意味はそれほどありません。シンプルにボンフェロー二の補正を行えばいいのです。スローガンは「英語教育研究は黙ってボンフェローニ!」です。
4つ目に,検定力分析によって大きな標本サイズを計画することを促進させるはずです。しかし,そもそも検定力分析自体やボンフェロー二の補正したαによる検定力分析が一般化していません。検出力について次回の記事で書きます。
なので,査読者はどうしても仮説のあり方が論理和的であり,さらに記述統計による探索的な態度ではすまない研究の場合,ボンフェロー二の補正を推奨するとよいかと思います。それ以外の方法の場合,査読者はもちろん,一般的な読者にとっても理解しにくい論文になる可能性もあります。査読プロセスの簡素化も大事な理由です。
考えておきたいこと
最後に,考えておきたいことをいくつかまとめます。
まず,いつもこのパターンですが,いわゆる数理モデルを構築し,近似度や適合度といったモデル評価の手続きによって,実質的には多重比較と同じ目的を達成することができる場合があります。ベイズ統計を使った実践では,もちろん場合によりますが,多重比較によるFWERの制御について考えなくてもよい場合もあります。
次に,次回の効果量の話と関わりますが,特に統計改革後において,「とにかく効果量だけを報告すればよい」であるとか「信頼区間だけ見ればよい」といった方針が聞かれるときもありました。もちろん,効果量や信頼区間は当然報告すべきであり,値も十分に吟味すべきです。しかし,これはあくまでも記述的な,または探索的な方法であると考えた方がよく,具体的な仮説や研究仮説とは馴染みません。たとえば「項目1,項目4,項目8の効果量が大であったことからこの理論が支持された」といった判断や,またはそのような「解釈」はあまりに危険です。詳しくは次回の記事をご覧ください。
また,α水準をもつ信頼区間も,「ある閾値が信頼区間内にあるかないか」の判断を複数行うときには,検定の多重性と同じ問題が原理的に発生します。厳密に言えば,信頼区間の水準も調整する必要があるというわけです。
最後に,蛇足になりますが,個人的な感情について述べます。この問題には非常に強い思い入れを持っているのです。自分が勉強する内容の側に,なぜか常にこの問題があり続けたのです。英語教育研究の発展を考えるすべての時間,必ずこの問題が私の頭に浮かぶのです。でも,本当に,この問題はもうそろそろやめにしませんか。どうにかこの記事が広まり,議論が深まることを期待するばかりです。そして,この記事がこの問題を考えさせてくれた先輩研究者*5たちの意図に沿うものであることを祈るばかりです。
サドコマシリーズ10箇条
…さて,と!これで新しいあいことばが増えました!
- 報告不備には生データ
- null resultsも評価する
- 検定の多重性は研究仮説を見る
次回は効果量について書きます!(現在は従来予定していたペースよりもだいぶ早めに公開しています)
私はSNSなどをやっておりませんので,どんどんシェアしていただくと幸いです!広くいろんな方に読んでいただけるよう一生懸命書いてます!
*1:ここでいうfamilyとは帰無仮説の集まり,帰無仮説族のことです
*2:永田靖・吉田 道弘(1997)『統計的多重比較法の基礎』サイエンティスト社.
*3:水本篤(2009)「複数の項目やテストにおける検定の多重性: モンテカルロ・シミュレーションによる検証」Language Education & Technology, 46, 1-19.
*4:草薙邦広・田村祐 (2017) 「外国語教育研究における事後分析の危険性」『外国語教育メディア学会中部支部外国語教育基礎研究部会2016年度報告論集』30-49.
*5:2008年くらいでしたが,私はある故人の先生のHPを見て,この問題を知りました。そのページでは非常にやさしく,わかりやすく,そしてユーモアを交えてこの問題を解説していました(私とは大違いです)。この先生のHPを見ているうちに,英語教育研究におけるデータ分析の実践一般に疑問と憤りを覚え,私は日に日に方法論に夢中になっていきました。それから時間が経って,こちらは名前を出させてもらいますが,関西大学の水本先生は,この問題を取り上げられて2010年に画期的な論文を執筆されました。モンテカルロ・シミュレーションを使った研究でした。「モンテカルロ・シミュレーションなんて名前がかっこいい」なんて思っているうちに,ブートストラップだのマルコフ連鎖モンテカルロ法だのを覚えました。そして,時代は変わっても,いつも私の前には「多重比較どうしたらいい?」という相談が来続けます。この記事を執筆している一週間くらいの間にもメールが1通来ました。本当に,「また,お前か…」です。先輩研究者たちも同じ轍を踏んでいたのでしょうね。