混合正規指数合成分布モデル（？）を最尤法で…

聞いたこともないけど，要素数2の混合正規指数合成分布（ex-Gaussian）モデルというのを考えてみる。ま，2つの異なる認知プロセスが混合したときの反応時間の分布だとか，そんなそれっぽいことを考えてみる。そんなものは多分ない。

ま，でもこの確率密度関数は，

dmixexgauss<-function(x,lambda,mu1,sigma1,tau1,mu2,sigma2,tau2){
	y<-lambda*(1/tau1)*exp(mu1/tau1+(sigma1^2)/(2*tau1^2)-x/tau1)* pnorm(x,mu1+(1/tau1)*sigma1^2, sigma1)
+(1-lambda)*(1/tau2)*exp(mu2/tau2+(sigma2^2)/(2*tau2^2)-x/tau2)* pnorm(x,mu2+(1/tau2)*sigma2^2,sigma2)
return(y)
	}

こうなはず。これで尤度関数を作って，bbmleパッケージのmle2とかで最尤推定してみれば…と思ったんだけど，やっぱ上手く推定できなかった。methodもBFGSとかいろいろ試したけど，ううむ。なんと7母数の確率密度関数だもんな。俺の間違いってのもあるし。

ま，でもこの自作の確率密度関数自体はあってるぽい。暇ができたらちょっとやってみよう。

library(retimes)
set.seed(1)
dat<-c(rexgauss(400,1000,300,800),rexgauss(100,4000,800,500))
hist(dat,main="",breaks=20,col="lightblue",freq=F,ylim=c(0,.0006),xlim=c(0,8000))
x<-seq(0,8000,1)
lines(x,dmixexgauss(x,.80,1000,300,800,4000,800,500),lty=2,col=2)

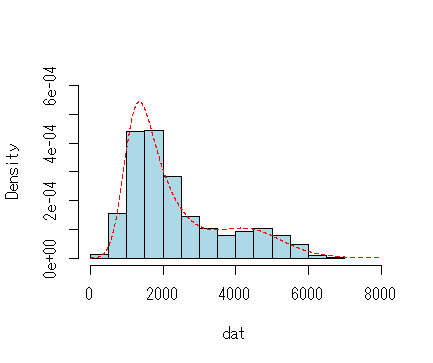
＊追記（1/28）
標本サイズ，母数，初期値次第では結構うまくいく場合もあるようだ。たとえば，

#あからさまな例
set.seed(1)
dat<-c(rexgauss(500,1000,500,100),rexgauss(500,10000,500,100))

#mle2で最尤推定
#対数尤度を返す関数
lf<-function(l,m1,s1,t1,m2,s2,t2){
-sum(log(dmixexgauss(dat,l,m1,s1,t1,m2,s2,t2)))
}

#適当な初期値で最尤推定
fit<-mle2(lf,start=list(l=.01,m1=1000,s1=100,t1=100,m2=10000,s2=100,t2=100))
summary(fit)

Maximum likelihood estimation

Call:
mle2(minuslogl = lf, start = list(l = 0.01, m1 = 1000, s1 = 100, 
    t1 = 100, m2 = 10000, s2 = 100, t2 = 100))

Coefficients:
     Estimate Std. Error  z value     Pr(z)    
l  5.0001e-01 1.5811e-02  31.6234 < 2.2e-16 ***
m1 8.8352e+02 5.3678e+01  16.4598 < 2.2e-16 ***
s1 4.2277e+02 2.8256e+01  14.9618 < 2.2e-16 ***
t1 2.5258e+02 5.1428e+01   4.9114 9.043e-07 ***
m2 9.8383e+03 5.6083e+01 175.4242 < 2.2e-16 ***
s2 4.4467e+02 2.8829e+01  15.4245 < 2.2e-16 ***
t2 2.4854e+02 5.3408e+01   4.6536 3.263e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

-2 log L: 16646.24 

coef(fit)
vcov(fit)
AIC(fit)