単変量の分布母数の推定からあれこれ:fitdistrplusパッケージが便利
ある確率分布を手持ちの単変量データに当てはめ,その母数を最尤推定するという方法があって,Rでは通常MASSパッケージのfitdistr関数を使うのがお手軽なんだけど,fitdistrplusという便利なパッケージが出ていてこれがとてもいいかも。ま,結局はoptimにかぶせているだけだが。
例えば,
- さまざまな可視化
- ブートストラップ
- 任意の母数を固定した状態での別の母数の推定
- 最尤推定以外の方法
- 適合度比較
みたいなのをかなり手軽にやってくれる。いちいち自分で書かなくてもいい。
可視化
たとえば,可視化に関してならば,
#数値例の作成 library(fitdistrplus) dat<-rgamma(300,2,3) #分布の確認 hist(dat) plot(ecdf(dat)) #これをガンマ分布に当てはめてみる fit<-fitdist(dat,"gamma") plot(fit) summary(fit)

ほら,便利。これだけ。
左上は,ヒストグラムに推定された母数の値を項にもつ確率密度関数。
右上はQ-Qプロット。この例だと,何故か大きい値があんま当てはまっていないことがわかる。
左下は経験累積密度関数と推定された母数の値の累積密度関数。右下はP-Pプロット。
もちろん,summaryも見やすい。こんな感じで普通欲しいのは一気に出してくれる。
Fitting of the distribution ' gamma ' by maximum likelihood Parameters : estimate Std. Error shape 1.965111 0.1488415 rate 2.841928 0.2450182 Loglikelihood: -156.0496 AIC: 316.0992 BIC: 323.5068 Correlation matrix: shape rate shape 1.0000000 0.8785199 rate 0.8785199 1.0000000
対数尤度プロットなる機能もある。これは,2つの母数の組み合わせの尤度をヒートマップみたいにしたのね。
尤度関数の2次元版,みたいなもんだろうか。ガンマは二母数だからね。
llplot(fit)

ブートストラップ
ブートストラップで誤差や信頼区間の検討もお手軽にできる。
fit<-fitdist(dat,"gamma") #B=1000でパラメトリック bfit1<-bootdist(fit,bootmethod="param",niter=1000) #B=500でノンパラメトリック bfit2<-bootdist(fit,bootmethod="nonparam",niter=500) #結果の表示 summary(bfit1) summary(bfit2)
ここではブートストラップした値の中央値と2.5%と97.5%点を出してくれる。←これはパーセンタイル法でのブートストラップ信頼区間でもある。
結果を色々見るには,
#パーセンタイル法での信頼区間 bfit1$CI #ブートストラップ推定値 boot.shape<-bfit1$estim[,1] boot.shape boot.rate<-bfit1$estim[,2] boot.rate #これをヒストグラムで描いて,中央値,パーセンタイル信頼区間を描き入れる。 par(mfrow=c(1,2)) hist(boot.shape,col="lightgray") abline(v=quantile(boot.shape,c(0.025,.5,.975)),col=2) hist(boot.rate,col="lightgray") abline(v=quantile(boot.rate,c(0.025,.5,.975)),col=2)

片方の母数を固定してもう片方の母数を最尤推定
やりたかったのこれ。ある理論的な見地から,片方の母数,例えば形状母数を任意の値に固定した状態で尺度母数を推定したいとか,これって結構外国語教育研究的によくあること。こういうときは,
#形状母数を無理やり3に固定(ホントは2) fitfix<-fitdist(dat,"gamma",method="mle",fix.arg=list("shape"=3)) #結果を見る summary(fitfix) Fitting of the distribution ' gamma ' by maximum likelihood Parameters : estimate Std. Error rate 4.525801 0.15086 Fixed parameters: value shape 3 Loglikelihood: -149.1229 AIC: 300.2459 BIC: 303.9496 #1つだから尺度母数のみの対数尤度曲線が出る llplot(fitfix)
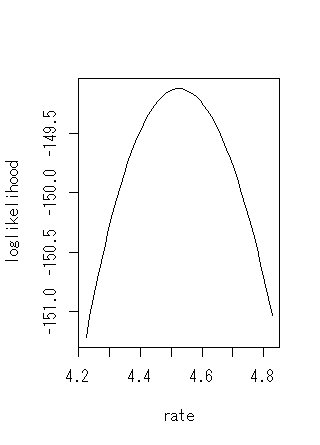
最尤推定以外の推定方法
最尤推定以外の方法も実装されている。methodに入れてやればいい。
- mle 最尤推定。もちろん初期値も与えられるし,optimの方法も指定できる
- mme モーメント法
- qme 分位点法
- mge 最大適合度法 よく知らない
fitfist(dat,"gamma",method="mme") fitfist(dat,"gamma",method="qme") fitfist(dat,"gamma",method="mge")
適合度比較
件のデータを,ワイブル,対数正規分布にも当てはめてみて,適合度を比較する。
#フィットさせる gam<-fitdist(dat,"gamma") weib<-fitdist(dat,"gamma") logn<-fitdist(dat,"lnorm") #比較(リストで入れる) gofstat(list(gam, weib, logn), fitnames=c("gamma", "Weibull", "lognormal")) #結果 goodness-of-fit statistics gamma Weibull lognormal Kolmogorov-Smirnov statistic 0.04626154 0.04626154 0.08208341 Cramer-von Mises statistic 0.05906861 0.05906861 0.43467475 Anderson-Darling statistic 0.40584196 0.40584196 2.93641451 Goodness-of-fit criteria gamma Weibull lognormal Aikake's Information Criterion 278.3222 278.3222 321.8015 Bayesian Information Criterion 285.7298 285.7298 329.2090
こんな感じ。便利ね。コルモゴロフ・スミルノフやアンダーソン・ダーリング検定ってのはわかる。残りのクラメール・フォン=ミーゼスってのは,こんなこと?なるほど。
Cramér–von Mises criterion - Wikipedia
…ま,最初はこうやってモデリングについて慣れていくことが大事で,こういうのがまさに出発点って感じだなあと最近しみじみ。