「反応時間がはやい」のカテゴリー錯誤
2018年もまた見てしまった…
はやい反応時間という表現。これが,外国語教育研究を含むある種の学術領域において,かなり慣習的な表現になっていることは知っている。たとえば,google scholarで以下のような表現を検索してみると,かなりの件数が表示される。興味ある方は試して欲しい。
- 早い反応時間
- 速い反応時間
- 遅い反応時間
- 早い応答時間
- 速い応答時間
- 遅い応答時間
- fast response time
- fast reation time
- slow response time
- slow reaction time
- fast response latency
- slow response latency
日本語に限ったことでなくて,英語だと数千件ずつヒットするような具合だ。このような表現が慣習的に使用されていることは紛れもない事実だとしても,このような表現に私は違和感を感じる。そして,非常に誤解を招きやすい危険な表現だと思う。ちょっとここでこれに関連することを整理したい。
速さ,道のり,時間
速さ(speed)は,単位時間あたりの物体の位置の差(距離)だ。小学校で誰もが学習するように,速さ=道のり÷時間。反応時間は,名前がまさにそれを示すように時間なのだから,時間に対して速いという形容詞は,厳密にいえばカテゴリー錯誤だ。時間は長短という性質をもち,速さは速いか,遅いかだ。まちがった形容詞を名詞につけている。
反応時間の単位は,大抵の場合,秒か,ミリ秒。記録を終えた時刻から記録を始めた時刻を引いたものが反応時間。一方,速さの単位は,分子にある道のり。ある一定の時間あたりに,どれだけ位置に差が生じたかということ。
たとえば,道のりをこなす課題の量だと考えるとわかりやすい。単語が擬似語かを判断する課題をさせるとして,1分間あたりに50試行,これはまさに単位時間あたりのこなした量なので速さ。1分間あたりに50試行は,1分間あたりに25試行より速い。
一つ目のややこしさ:それぞれの関係
ただし,厄介なのが,道のり(に例えられる課題量や認知メカニズム?)が等しいと考えられるとき,そういう特殊な条件の下では,その道のりを移動し終える(課題を完遂する,認知メカニズムを終了する)までの時間が短ければ必然的に速く,その時間が長ければ必然的に遅い,といえるかもしれない。
日常言語であまり使い分けられているとはいえないけれど,速さ(speed)と速度(velocity)と早さ(earliness)は厳密にいえば異なることだと思うひともいる。学校でならったことによれば,速さはスカラーで,速度はベクトルだ。この区別はまだしも,早さは,ある事象の生じた時刻などが相対的に前のほうであるということだ。スタート時刻が一緒で,1kmを複数人が走るとしたとき,ほかのひとよりも早く着くひとがいる。このとき,その早く着いたひとは速く走るのかもしれないし,この条件下で着くまでの時間が短ければ早く着いて速く走るのかもしれない。非常にややこしい。落ち着いて考えたいところだ。しかし,早い反応時間というようないい方の違和感は変わりない。過去に自分もそのように書いてしまった論文があるのだけども。
二つ目のややこしさ:潜在変数と観測変数
もっともやっかいなことは,潜在変数と観測変数の関係,または操作化についてのこと。一般に,潜在変数としてなにかの技能や知識があって,反応時間はその潜在変数の影響を受ける観測変数として考えられることがある。たとえば,英語の読解力というものが少なくても心理測定的な含意のもとで存在するとされ,読解力(という名の潜在変数の値)が高ければ英語を読むのが速い(または読解力が高いひとは,そうでないひとよりも英語を読み終えるのが早い,または読解力が高いひとが示す読解時間は,そうでない人が示すそれよりも短い)といった関係性。または,かなり乱暴に操作化という手続きをして,反応時間は読解能力であると読み替えるかもしれない。この関係性や操作化による読み替えがカテゴリー錯誤の原因かもしれない。
たとえば,研究者のなかに,読解力=反応時間というような置き換え規則があって,さらに,読解力が処理の速さ(processing speed)という側面をもつなどという理論的な先行研究を参照してたりしたら,読解力,つまり処理の速さは反応時間だから,反応時間が速い,というようないい方をついついしてしまうのかもしれない。つまり,読解力やそれに類するカテゴリーの性質を,反応時間という,まったく異なる性質をもつものに転移させているわけ。つまり,潜在変数がもつ性質と観測変数がもつ性質をごっちゃにしている。
できればこのようないい方を避けたい。これは論文全体の解釈にも影響を及ぼすことなので。
安全ないい方
既存の確立された学術領域における標準的な言葉遣いを避けることがよいことかはわからないけども(たぶんよくない),それでも,あくまでも反応時間に関しては,長短と書く方が無難かもしれない。
たとえば,(有意に長いとか短いとかはoutdatedだと思うけども)
- 条件Aにおける反応時間の平均値は,条件Bにおけるそれよりも有意に短い。
- 条件Aにおける反応時間の平均値は,条件Bにおけるそれよりも有意に長い。
または,もっとも安全で,そして汎用的な表現は,
- 条件Aにおける反応時間の平均値は,条件Bにおけるそれよりも大きな値を取った。
- 条件Aにおける反応時間の平均値は,条件Bにおけるそれよりも小さな値を取った。
これはこれで値が大小なのか高低なのかという問題があるけども,確率変数では最小値と最大値などともいうので,少なくとも変数の期待値を大小でいってもいいだろうと思う。英語では,greaterなどといえばいいかもだ。なんでも単位や形容詞が不安なときは,これが安パイ。
逆に,速いまたは早いを使うのだとしたら,
- 反応が速い
- 早く完了する
などといったいいかたの方が誤解を招かないかも。
うん。
カーブフィッティング+ブートストラップ
また懲りずにMenzerath-Altmann法則の話。こんなデータがあって,
| Morpheme Length(Syllables) | Syllable Length(Phonemes) |
| 1 | 3.10 |
| 2 | 2.53 |
| 3 | 2.29 |
| 4 | 2.12 |
| 5 | 2.09 |
Gabriel Altmann (1980). "Prolegomena to Menzerath's law". Glottometrika. 2: 1–10.
これがこの方程式にフィットするという観測的事実がある。
(a)
これを非線形最小二乗でやるのが普通なんだけど,今日はこれをブートストラップするという話。
MCMCやった後になんだけど,使うRパッケージは,nlstools。
#パッケージ読み込み libarary(nlstools) #データ入力 s<-1:5 m<-c(3.1,2.53,2.29,2.12,2.09) dat<-data.frame(s,m) #モデルをフィット fit<-nls(m~a*s^(-b)*exp(1)^(-c*s), start=list(a=3,b=0,c=0), data=dat) #ブートストラップ(B = 1,000)する boot.fit<-nlsBoot(fit,1000) #パーセンタイル法で誤差を見る summary(boot.fit) #適当にカーネルで可視化 plot(density(boot.fit$coefboot[,1]),main="a",type="n") polygon(density(boot.fit$coefboot[,1]),col="lightblue") plot(density(boot.fit$coefboot[,2]),main="b",type="n") polygon(density(boot.fit$coefboot[,2]),col="pink") plot(density(boot.fit$coefboot[,3]),main="c",type="n") polygon(density(boot.fit$coefboot[,3]),col="lightgreen")

うっす。
言語法則とベイズ的なカーブフィッティング
続きもので書いていたつもりだったのだけど,放置しすぎて前回からの更新間隔がえげつないことになってしまった。前回は,
Menzerath-Altmann法則をRのnls関数で - 草薙の研究ログ
っていう話だった。えっと,「ある言語学的単位の平均長(y)は,その構成要素の長さ(x)の関数である」っていう古典的な観察があって,具体的には,この関数,
(a)
に従うだろう,という話だ。これをMezerath-Altmann法則と呼ぶんだそう(Altmann, 1980)。こういう言語法則系は話がとってもシンプルでいい。
たとえば,こんなデータ(Altmann, 1980)。
| Morpheme Length(Syllables) | Syllable Length(Phonemes) |
| 1 | 3.10 |
| 2 | 2.53 |
| 3 | 2.29 |
| 4 | 2.12 |
| 5 | 2.09 |
図にするとこんな感じ。確かに指数的減衰する関数ならフィットしそうだ。

普通に非線形最小二乗法でフィッティングしてもいいんだけど,世の中にはベイズ的なカーブフィッティングとかそういうのがあるそうで,RではFMEパッケージでそれができるんだそう。やってみよう。
これはメトロポリス法によって…とかそういう細かいところはぜんぶ置いといて(よくわからんし),まあこんな感じか。
#データ s<-1:5 m<-c(3.1,2.53,2.29,2.12,2.09) #モデルを書く Model <- function(p, x) { data.frame(x = x, N = p[1]*s^(-p[2])*exp(1)^(-p[3]*s)) } Residuals <- function(p) { (m - Model(p,s)$N) } #まずはパッケージの例通りにやってみる P <- modFit(f = Residuals, p = c(0,0,0)) sP <- summary(P) Covar <- sP$cov.scaled * 2.4^2/2 s2prior <- sP$modVariance MCMC <- modMCMC(f = Residuals, p = P$par,jump = Covar, niter = 5100, var0 = s2prior, wvar0 = NULL, updatecov = 100, burninlength=100) #トレース図とMCMCの結果を可視化 par(mfrow=c(2,3)) title<-c("a","b","c") for(i in 1:3){ plot(MCMC$par[,i],type="l", xlab="Iteration", ylab="", main=title[i]) } for(i in 1:3){ plot(density(MCMC$par[,i]), type="n", main=title[i]) polygon(density(MCMC$par[,i]), col="gray98") }

ほうほう。で,こんな感じになるというわけ。

Gabriel Altmann (1980). "Prolegomena to Menzerath's law". Glottometrika. 2: 1–10.
Menzerath-Altmann法則と一般化ガンマ分布(Eroglu, 2013)
とても興味深いこと。Eroglu(2013)は,Menzerath-Altmann法則と一般化ガンマ分布の関係について説明している。
Eroglu, S. (2013). Menzerath-Altmann law for distinct word distribution analysis in a large text. Physica A, 392, 2775 – 2780
Menzerath-Altmann法則は,
(a)
という風に書ける。
ここで,b = 0,c ≒ 0のとき,
(b)
となる。これは普通の指数関数。
で,b ≒ 0,c = 0のとき,
(c)
これはZipfの法則。
ここで,一般化ガンマ分布の確率密度関数を(d)のように書くとする(parameterizationもいろいろあるが…)。
(d)
β = 1のとき,(d)式はガンマ分布の確率密度関数になるし,β=θのとき,ワイブル分布の確率密度関数になる。その上,ガンマ分布は,母数の値によっては,指数分布にもなるし,アーラン分布にもなる。
で,いちばん大事なんだけど,のとき,(d)式は(a)式になるらしい(Eroglu, 2013, p. 2776)。なるほど。
…なんだか,とっても安心する。
Menzerath-Altmann法則をRのnls関数で
Menzerath-Altmann法則(またはMenzerath法則; e.g., Altmann, 1980; 基本的アイデアはMenzerathが発見,Altmannが定式化)とは,ある言語学的単位の増加が,その単位の構成要素の減少に帰着すること。またはその逆。
もっと一般的にいうと,Altmann(1980)は,「ある言語学的単位の長さは,その構成要素の長さの関数である」としている。たとえば,ある形態素長(形態素内の音節数などとして測定する)の値が高ければ,その形態素内の平均的な音節長(音節内の音素の数などとして測定される)の値は低くなるということ。ある言語において,1音節からなる形態素の平均的な音素数は3,2音節からなる形態素(ひとつつあたりの)の平均的な音素数は2.5,3音節からなる形態素の平均的な音素数は2…というように。
それで,基本的にはさまざまな単位,たとえば時間などでもこの法則が当てはまるとされ,実証研究も少なくないし,ゲノムとかタンパク質とか,そういう分野にも応用されているんだそうだ。で,その関係は,簡単な方程式で表されると。
もっとも一般的な式は,
(a)
ここでのyは構成要素(小さい方)の長さ,xは対象とする言語学的単位の長さ,a,b,cは自由母数。eはネイピア数。この式を使い,観測から,a,b,cを推定する,というわけだ。
一番単純な方法だと,最小二乗法を使用することができる。
Rには,非線形最小二乗法用の関数nlsがあるので,これを使えばいい。Altmann(1980)にインドネシア語の形態素と音節の関係についてのデータが示されている。これは,こんな感じ。
Gabriel Altmann (1980). "Prolegomena to Menzerath's law". Glottometrika. 2: 1–10.
| Morpheme Length(Syllables) | Syllable Length(Phonemes) |
| 1 | 3.10 |
| 2 | 2.53 |
| 3 | 2.29 |
| 4 | 2.12 |
| 5 | 2.09 |
やってみる。
#データ入力 s<-1:5 m<-c(3.1,2.53,2.29,2.12,2.09) #可視化 plot(s,m,xlab="Morpheme Length",ylab="Syllable Length",pch=20,cex=2) #モデルをフィット fit<-nls(m~a*s^(-b)*exp(1)^(-c*s),start=list(a=3,b=0,c=0)) #サマリーなど summary(fit) AIC(fit) BIC(fit) #決定係数 cor(m,predict(fit))^2 #予測値をプロット plot(s,m,xlab="Morpheme Length",ylab="Syllable Length",pch=20,cex=2) points(s,predict(fit),col=2,pch=20)
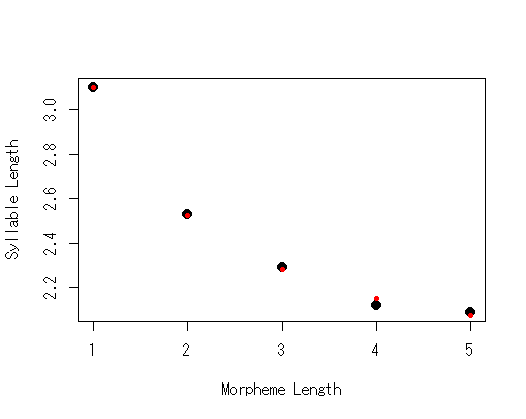
赤がモデル理論値。もちろん原著の推定結果ともほぼ一致している。
このデータでは,以下のようになった。
(b)
この法則がどれだけ法則と呼ぶに相応しい一般化可能性をもつかといった面と,具体的に(a)式がどれだけ観測にフィットするかということは置いといて,ある単位と,その構成素の関係に一般的な法則をもとめる姿勢というのは,とても正当な考え方だと思う。
ジニ係数とワイブル分布・対数正規分布・ガンマ分布の母数の関係
どうでもいいことなんだけど,ジニ係数はいくつかの分布であれば,分布の母数から直接的にもとまるんだそうだ。
ワイブル分布,対数正規分布,ガンマ分布を例に取ると,ワイブル分布とガンマ分布なら形状母数k(またはα)のみから,対数正規分布ならσのみから直接ジニ係数がもとまる。これらを計算するRの関数を作ってみる。
#ガンマ分布 gamma.gini<-function(a){ gini<-gamma((2*a+1)/2)/k/gamma(a)/sqrt(pi) gini } #ワイブル分布 weibull.gini<-function(k){ gini<-1-2^(-1/k) gini } #対数正規分布 lognorm.gini<-function(s){ gini<-2*pnorm(s/2*sqrt(2))-1 gini }
あるデータの分布がワイブル分布に従っているとして,その形状母数kが2だったとしたら,
weibull.gini(2) 0.2928932
この関数にはベクトルを入れられるので,こんなグラフも作れる。

x<-seq(0.1,5,.01) plot(x,weibull.gini(x),xlab="Parameter",ylab="Gini Coefficient",type="l")
ワイブル分布では,形状母数が大きくなればなるほどジニ係数は小さくなる。
…どうでもいいことなんだけど,ワイブル分布の形状母数について,MCMCのサンプルを得て,ジニ係数の信用区間を得ることもできるんじゃないだろうか。たとえば,
set.seed(1) d<-rweibull(1000,3,1) library(MCMCpack) llf<-function(beta,x){ sum(log(dweibull(x,beta[1],beta[2]))) } m<-MCMCmetrop1R(llf,theta.init=c(3,1),x=d) gini<-weibull.gini(m[,1]) plot(density(gini),type="n",xlab="Gini",ylab="Density",main="") polygon(density(gini),col=rgb(0,0,1,.2)) #信用区間 quantile(gini,c(.025,.975)) 2.5% 97.5% 0.1963506 0.2140616
こんな感じで。

みたいな。
GAMLSSとBAMLSSで分布をデータにフィット
GAMLSSとBAMLSS
新幹線に乗ってコンビニにいくようなものだけど,GAMLSSとそのベイズ的モデルであるBAMLSSを使って,観測のデータに対して分布をフィットさせる。
GAMLSSというのは,「位置,尺度,形状,それぞれの母数のための一般化加法モデル(Generalized additive model for location, scale and shape)」のこと。詳しくはwikiや,開発者らのページを。
Generalized additive model for location, scale and shape - Wikipedia
gamlss | for statistical modelling
大雑把にいえば,分布ベースの回帰モデルのひとつ。
基本的には,(ひとつの)応答変数になんらかの分布を仮定する。正規分布とかガンマとか。
たとえばガンマ分布だったら,α(形状)とβ(比率)母数のふたつがあると。
で,応答変数のそれぞれの値は,これらの母数によってランダムに発生していると。
GAMLSSでは,これら,それぞれの母数の値自体を予測する。
予測変数の値という条件における,応答変数が従うであろう分布の母数を予測して,そこから応答変数ができてるみたいな。
この母数に対する予測は,線形な関係であってもいいし,加法モデルというくらいだから,スプラインとかでもいい。
基本,4母数までの分布ならできるらしく(μ,σ,ν,τ),Rのgamlssパッケージには莫大な数の分布がサポートされている。
変量効果も入れられる。とっても自由。
BAMLSSというのは,これとほぼ同じようなことをベイズ的にやるんだそうだ(細かい事前分布の設定とかアルゴリズムはよくわからない)。
これが面白いのは,平均値を予測するだけでなくて,散布度や形状を予測することができるようになるところ。
たとえば,実験条件Aは,応答変数の平均値には影響を及ぼさないけど,分散を大きくする効果をもつ,とか。
歪んだ分布を仮定して,実験条件Bは,応答変数の形状に影響を及ぼす,とか。そういうモデリングができるようになる。
「分位点回帰のパラメトリック版を非線形でもできるようにしてる」,みたいな感じ。
…それは置いておいて,このパッケージは特に便利なので,まずは単変量の分布の母数をこれらのパッケージで推定する。
ある分布に従う単変量の母数の推定
MASSパッケージのfitdistrやfitdistrplusパッケージでもoptim関数でも,なんなら場合によってはglm関数でも,同じことをやることができる場合は多いのだけど,gamlssパッケージやbamlssパッケージは,普通に単変量のデータの分布を推定できる。
まずは,データにワイブル分布を当てはめて母数を推定する例をやってみる。
#読み込み library(gamlss) #データの作成 set.seed(92) d1<-rweibull(1000,2,1) #gamlssの基本関数を使って推定 #最初の回帰式がμ(最初の母数),次の回帰式をσと当てている使用 WEIは,ワイブル分布 m1<-gamlss(d1~1,sigma.formula=~1,family="WEI") #これでダン #サマリーしてみる summary(m1)
切片の推定値はそれぞれ,μ(ここでは尺度母数) = -0.01,σ(ここでは形状母数) = .677くらい。
これにはリンク関数としてlogが噛んでいるので,係数をexpする。
すると,まあ,1と2くらい。よく推定できている。もちろん,これはただの最尤推定と同じなので,他のパッケージとかとも一致する。
で,もっと楽な関数があって,gamlssMLという最尤推定の関数。
m2<-gamlssML(d1,"WEI") summary(m2)
これもおなじことになる。わざわざ切片からの回帰式とか書かなくてもよい。
もっと便利なのがあって,histDistという関数。
これは,ヒストグラムとフィットした確率密度曲線を描いてくれるだけでなくて,上のサマリーも返してくれる。
histDist(d1,"WEI")
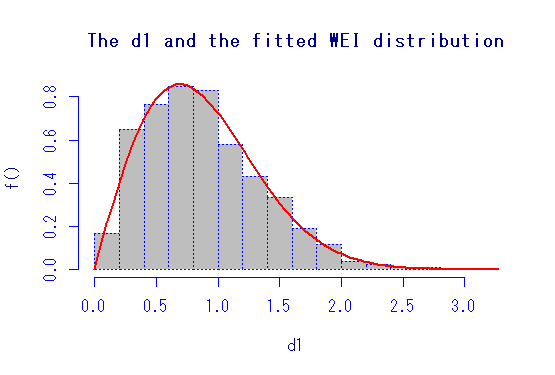
図はこんな感じ。オプションもあるので,色々いじれるけど,自分はやらないだろうな。
BAMLSSでも基本は同じ。少なくともこの状態で,それぞれの事前分布は基本的に無情報っぽい。
MCMCサンプラーはJAGSとか色々指定できるみたいだけど,デフォルトではGMCMCというのを使っているそう(これはよくわからない)。
library(bamlss) #いろいろなオプションを省略して… m3<-bamlss(list(mu=d1~1,sigma=~1),family="weibull") summary(m3)
それぞれの母数の95%信用区間(パーセンタイル法)も出してくれる。
以下のようにしたら,MCMCサンプルも可視化できる。
par(mfrow=c(1,2)) plot(density(exp(unlist(m3$s[,1]))),main="Scale",xlab="Value") plot(density(exp(unlist(m3$s[,5]))),main="Shape",xlab="Value")
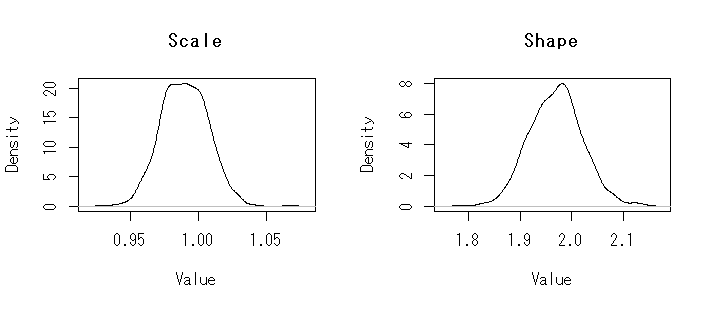
簡単なモデル
えっと,せっかくだから,ただ生データをフィットさせるだけでなくて,GAMLSSやBAMLSSの中でも,もっとも簡単な回帰モデル的なものをやってみよう。
アイリスデータの,がく片の長さ(sepal length)を応答変数,あやめの種類(3水準)を予測変数としよう。がく片の長さは正規分布に従うとして,種類は,がく片の長さの平均と標準偏差にそれぞれどのような影響をあたえるだろうか。ここであやめの種類はfactor型。
データとしてはこんな感じ。
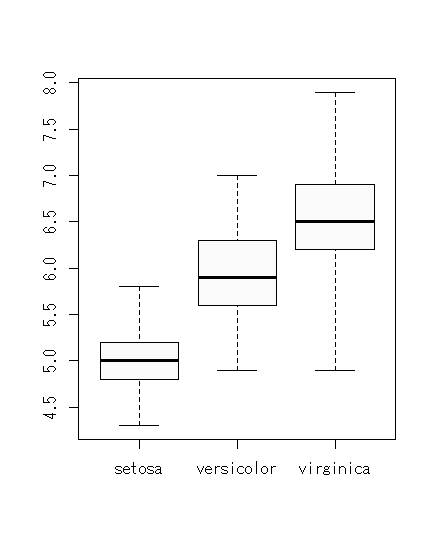
見た感じ,平均はsetosa < versicolor < virginicaという大きさのようになっている。標準偏差も同じ。
普通の線形モデルなら,
summary(lm(iris[,1]~iris[,5])) anova(lm(iris[,1]~iris[,5]))
みたいにする。
一方,gamlssでは,こんな感じにする。
m4<-gamlss(iris[,1]~iris[,5],sigma.formula=~iris[,5],family="NO") summary(m4) ****************************************************************** Family: c("NO", "Normal") Call: gamlss(formula = iris[, 1] ~ iris[, 5], sigma.formula = ~iris[, 5], family = "NO") Fitting method: RS() ------------------------------------------------------------------ Mu link function: identity Mu Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 5.00600 0.04935 101.44 <2e-16 *** iris[, 5]versicolor 0.93000 0.08751 10.63 <2e-16 *** iris[, 5]virginica 1.58200 0.10179 15.54 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------ Sigma link function: log Sigma Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.0528 0.1000 -10.528 < 2e-16 *** iris[, 5]versicolor 0.3814 0.1414 2.697 0.00783 ** iris[, 5]virginica 0.5900 0.1414 4.172 5.2e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------ No. of observations in the fit: 150 Degrees of Freedom for the fit: 6 Residual Deg. of Freedom: 144 at cycle: 2 Global Deviance: 206.9715 AIC: 218.9715 SBC: 237.0353 ******************************************************************
普通の線形モデルと違って,標準偏差の大きさの違いも同時にモデリングしている。
まあ,見た感じの結果になっている。これは,こんな感じに可視化するとわかりやすい。
term.plotという関数もある。
par(mfrow=c(1,2)) term.plot(m4,"mu",main="Mu") term.plot(m4,"sigma",main="Sigma")
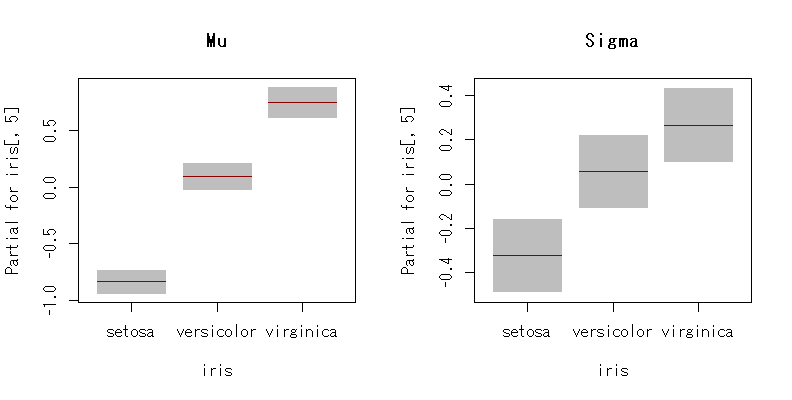
もちろん,診断プロットもある。
plot(m4)
それぞれの予測された母数から,確率密度曲線を描くとこんな感じ。
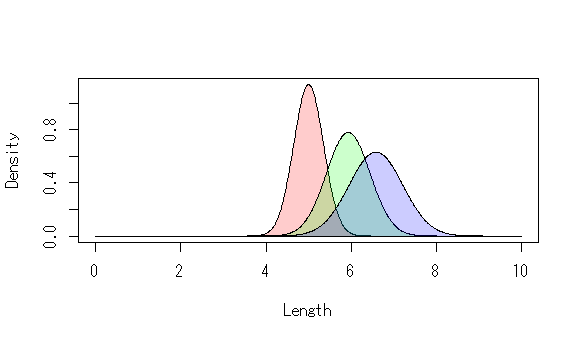
もちろん,標準偏差には影響を及ぼさないとか,標準偏差には影響を及ぼすけど,平均値には及ぼさない,といったモデルを作り,適合度を比較したり尤度比検定をしたりすることもできる。
まあでも,これ予測変数が因子型だったら,教師ありの混合分布モデルみたいなもん。
blmssパッケージでは,
m5<-bamlss(list(mu=iris[,1]~iris[,5],sigma=~iris[,5]),family="gaussian")
で,(当然だけど)同じような結果を得ることができる。MCMCサンプルを可視化したり,信用区間を構築してもよい。
とっても便利。
平均は変わらないけど,標準偏差だけ違う2群のモデル
回帰モデルは自由に作れるので,ある因子が標準偏差だけに影響を及ぼしているモデルとかも作れる。
たとえば,こんなデータだとしよう。
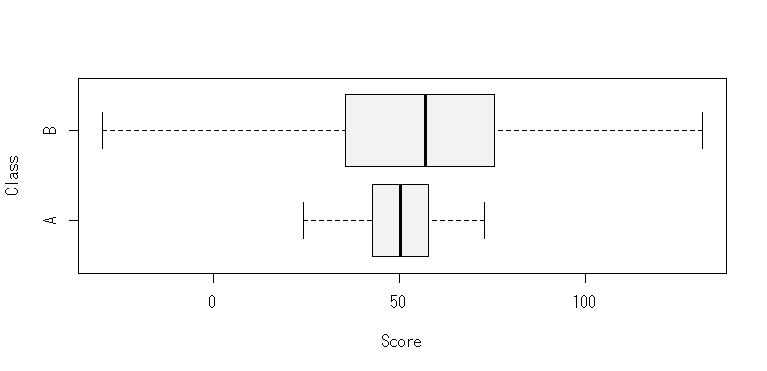
group<-as.factor(c(rep("A",100),rep("B",100))) score<-c(rnorm(100,50,10),rnorm(100,50,30)) d2<-data.frame(group,class) m6<-gamlss(score~1,sigma.formula=~group,data=d2) summary(m6) term.plot(m6,"sigma",main="Sigma")
結果はこんな感じ。
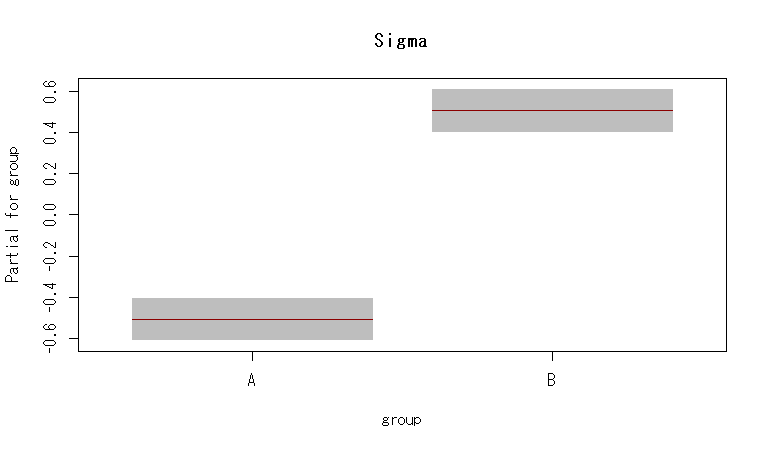
ちょっと複雑なモデル
えっと,実質的に意味があるかはわからないけど(ないだろう),がく片の長さの分布を正規分布だと仮定して,がく片の幅と花びらの長さから,その予測値という条件下における分布の母数(平均,標準偏差)を推定するとしよう。で,その予測値と予測される母数の関係は非線形だと。
#ここでは罰則付きスプラインの一種 m7<-gamlss(Sepal.Length~pb(Sepal.Width)+pb(Petal.Length),sigma.formula=~pb(Sepal.Width)+pb(Petal.Length),data=iris,family="NO") summary(m6) par(mfrow=c(2,2)) term.plot(m7,"mu",main="Mu") term.plot(m7,"sigma",main="Sigma")
可視化するとこんな感じ。
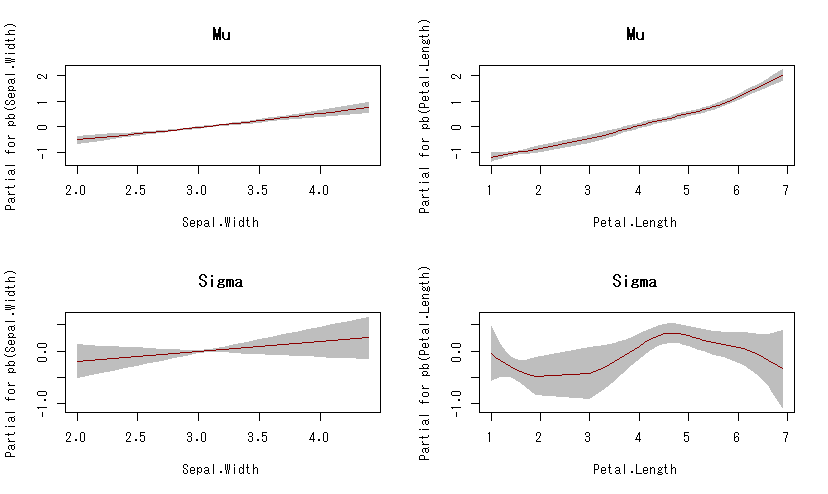
がく片の幅と花びらの長さが長くなれば,がく片の長さの分布における平均はそれぞれ単調に増加しそう(花びらの長さはちょっと指数的に見える)。
がく片の幅は,がく片の長さの分布における標準偏差とはあまり関係なさそうだ。しかし,花びらの長さは,がく片の長さの分布における標準偏差に非線形の影響を及ぼしているかも(意味ないと思うけど)。…みたいな。
で,これに種類を変量効果と考えて…というようにやっていくと,大分自由なモデリングができそう。
(最尤推定による分布のフィットから書き始めて,やっとここまで来たって感じ)