ジニ係数とワイブル分布・対数正規分布・ガンマ分布の母数の関係
どうでもいいことなんだけど,ジニ係数はいくつかの分布であれば,分布の母数から直接的にもとまるんだそうだ。
ワイブル分布,対数正規分布,ガンマ分布を例に取ると,ワイブル分布とガンマ分布なら形状母数k(またはα)のみから,対数正規分布ならσのみから直接ジニ係数がもとまる。これらを計算するRの関数を作ってみる。
#ガンマ分布 gamma.gini<-function(a){ gini<-gamma((2*a+1)/2)/k/gamma(a)/sqrt(pi) gini } #ワイブル分布 weibull.gini<-function(k){ gini<-1-2^(-1/k) gini } #対数正規分布 lognorm.gini<-function(s){ gini<-2*pnorm(s/2*sqrt(2))-1 gini }
あるデータの分布がワイブル分布に従っているとして,その形状母数kが2だったとしたら,
weibull.gini(2) 0.2928932
この関数にはベクトルを入れられるので,こんなグラフも作れる。

x<-seq(0.1,5,.01) plot(x,weibull.gini(x),xlab="Parameter",ylab="Gini Coefficient",type="l")
ワイブル分布では,形状母数が大きくなればなるほどジニ係数は小さくなる。
…どうでもいいことなんだけど,ワイブル分布の形状母数について,MCMCのサンプルを得て,ジニ係数の信用区間を得ることもできるんじゃないだろうか。たとえば,
set.seed(1) d<-rweibull(1000,3,1) library(MCMCpack) llf<-function(beta,x){ sum(log(dweibull(x,beta[1],beta[2]))) } m<-MCMCmetrop1R(llf,theta.init=c(3,1),x=d) gini<-weibull.gini(m[,1]) plot(density(gini),type="n",xlab="Gini",ylab="Density",main="") polygon(density(gini),col=rgb(0,0,1,.2)) #信用区間 quantile(gini,c(.025,.975)) 2.5% 97.5% 0.1963506 0.2140616
こんな感じで。

みたいな。
GAMLSSとBAMLSSで分布をデータにフィット
GAMLSSとBAMLSS
新幹線に乗ってコンビニにいくようなものだけど,GAMLSSとそのベイズ的モデルであるBAMLSSを使って,観測のデータに対して分布をフィットさせる。
GAMLSSというのは,「位置,尺度,形状,それぞれの母数のための一般化加法モデル(Generalized additive model for location, scale and shape)」のこと。詳しくはwikiや,開発者らのページを。
Generalized additive model for location, scale and shape - Wikipedia
gamlss | for statistical modelling
大雑把にいえば,分布ベースの回帰モデルのひとつ。
基本的には,(ひとつの)応答変数になんらかの分布を仮定する。正規分布とかガンマとか。
たとえばガンマ分布だったら,α(形状)とβ(比率)母数のふたつがあると。
で,応答変数のそれぞれの値は,これらの母数によってランダムに発生していると。
GAMLSSでは,これら,それぞれの母数の値自体を予測する。
予測変数の値という条件における,応答変数が従うであろう分布の母数を予測して,そこから応答変数ができてるみたいな。
この母数に対する予測は,線形な関係であってもいいし,加法モデルというくらいだから,スプラインとかでもいい。
基本,4母数までの分布ならできるらしく(μ,σ,ν,τ),Rのgamlssパッケージには莫大な数の分布がサポートされている。
変量効果も入れられる。とっても自由。
BAMLSSというのは,これとほぼ同じようなことをベイズ的にやるんだそうだ(細かい事前分布の設定とかアルゴリズムはよくわからない)。
これが面白いのは,平均値を予測するだけでなくて,散布度や形状を予測することができるようになるところ。
たとえば,実験条件Aは,応答変数の平均値には影響を及ぼさないけど,分散を大きくする効果をもつ,とか。
歪んだ分布を仮定して,実験条件Bは,応答変数の形状に影響を及ぼす,とか。そういうモデリングができるようになる。
「分位点回帰のパラメトリック版を非線形でもできるようにしてる」,みたいな感じ。
…それは置いておいて,このパッケージは特に便利なので,まずは単変量の分布の母数をこれらのパッケージで推定する。
ある分布に従う単変量の母数の推定
MASSパッケージのfitdistrやfitdistrplusパッケージでもoptim関数でも,なんなら場合によってはglm関数でも,同じことをやることができる場合は多いのだけど,gamlssパッケージやbamlssパッケージは,普通に単変量のデータの分布を推定できる。
まずは,データにワイブル分布を当てはめて母数を推定する例をやってみる。
#読み込み library(gamlss) #データの作成 set.seed(92) d1<-rweibull(1000,2,1) #gamlssの基本関数を使って推定 #最初の回帰式がμ(最初の母数),次の回帰式をσと当てている使用 WEIは,ワイブル分布 m1<-gamlss(d1~1,sigma.formula=~1,family="WEI") #これでダン #サマリーしてみる summary(m1)
切片の推定値はそれぞれ,μ(ここでは尺度母数) = -0.01,σ(ここでは形状母数) = .677くらい。
これにはリンク関数としてlogが噛んでいるので,係数をexpする。
すると,まあ,1と2くらい。よく推定できている。もちろん,これはただの最尤推定と同じなので,他のパッケージとかとも一致する。
で,もっと楽な関数があって,gamlssMLという最尤推定の関数。
m2<-gamlssML(d1,"WEI") summary(m2)
これもおなじことになる。わざわざ切片からの回帰式とか書かなくてもよい。
もっと便利なのがあって,histDistという関数。
これは,ヒストグラムとフィットした確率密度曲線を描いてくれるだけでなくて,上のサマリーも返してくれる。
histDist(d1,"WEI")
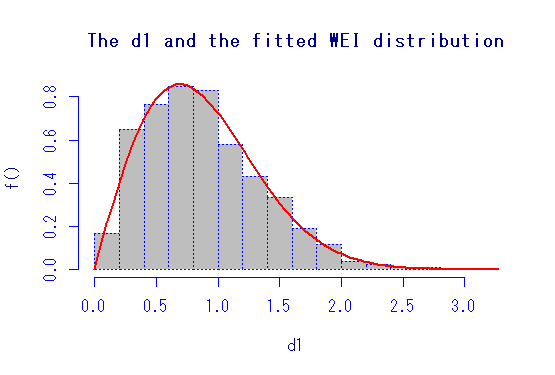
図はこんな感じ。オプションもあるので,色々いじれるけど,自分はやらないだろうな。
BAMLSSでも基本は同じ。少なくともこの状態で,それぞれの事前分布は基本的に無情報っぽい。
MCMCサンプラーはJAGSとか色々指定できるみたいだけど,デフォルトではGMCMCというのを使っているそう(これはよくわからない)。
library(bamlss) #いろいろなオプションを省略して… m3<-bamlss(list(mu=d1~1,sigma=~1),family="weibull") summary(m3)
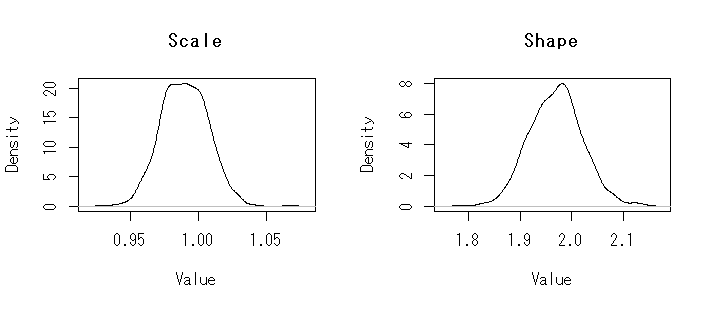
それぞれの母数の95%信用区間(パーセンタイル法)も出してくれる。
以下のようにしたら,MCMCサンプルも可視化できる。
par(mfrow=c(1,2)) plot(density(exp(unlist(m3$s[,1]))),main="Scale",xlab="Value") plot(density(exp(unlist(m3$s[,5]))),main="Shape",xlab="Value")
簡単なモデル
えっと,せっかくだから,ただ生データをフィットさせるだけでなくて,GAMLSSやBAMLSSの中でも,もっとも簡単な回帰モデル的なものをやってみよう。
アイリスデータの,がく片の長さ(sepal length)を応答変数,あやめの種類(3水準)を予測変数としよう。がく片の長さは正規分布に従うとして,種類は,がく片の長さの平均と標準偏差にそれぞれどのような影響をあたえるだろうか。ここであやめの種類はfactor型。
データとしてはこんな感じ。
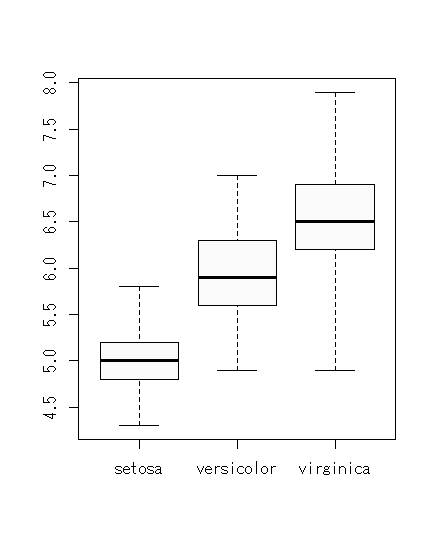
見た感じ,平均はsetosa < versicolor < virginicaという大きさのようになっている。標準偏差も同じ。
普通の線形モデルなら,
summary(lm(iris[,1]~iris[,5])) anova(lm(iris[,1]~iris[,5]))
みたいにする。
一方,gamlssでは,こんな感じにする。
m4<-gamlss(iris[,1]~iris[,5],sigma.formula=~iris[,5],family="NO") summary(m4) ****************************************************************** Family: c("NO", "Normal") Call: gamlss(formula = iris[, 1] ~ iris[, 5], sigma.formula = ~iris[, 5], family = "NO") Fitting method: RS() ------------------------------------------------------------------ Mu link function: identity Mu Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 5.00600 0.04935 101.44 <2e-16 *** iris[, 5]versicolor 0.93000 0.08751 10.63 <2e-16 *** iris[, 5]virginica 1.58200 0.10179 15.54 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------ Sigma link function: log Sigma Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.0528 0.1000 -10.528 < 2e-16 *** iris[, 5]versicolor 0.3814 0.1414 2.697 0.00783 ** iris[, 5]virginica 0.5900 0.1414 4.172 5.2e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------ No. of observations in the fit: 150 Degrees of Freedom for the fit: 6 Residual Deg. of Freedom: 144 at cycle: 2 Global Deviance: 206.9715 AIC: 218.9715 SBC: 237.0353 ******************************************************************
普通の線形モデルと違って,標準偏差の大きさの違いも同時にモデリングしている。
まあ,見た感じの結果になっている。これは,こんな感じに可視化するとわかりやすい。
term.plotという関数もある。
par(mfrow=c(1,2)) term.plot(m4,"mu",main="Mu") term.plot(m4,"sigma",main="Sigma")
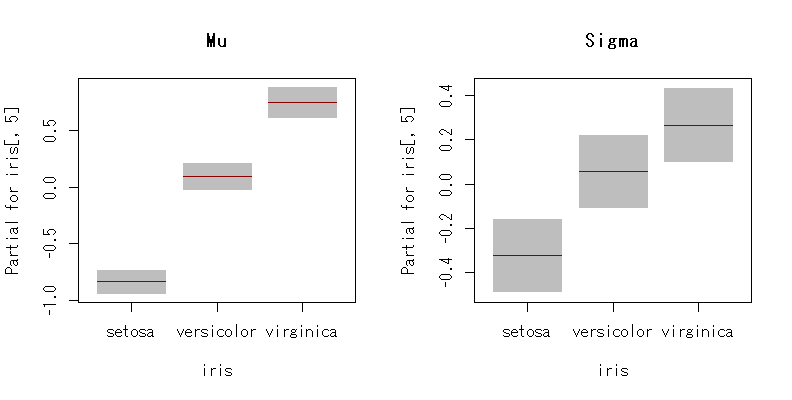
もちろん,診断プロットもある。
plot(m4)
それぞれの予測された母数から,確率密度曲線を描くとこんな感じ。
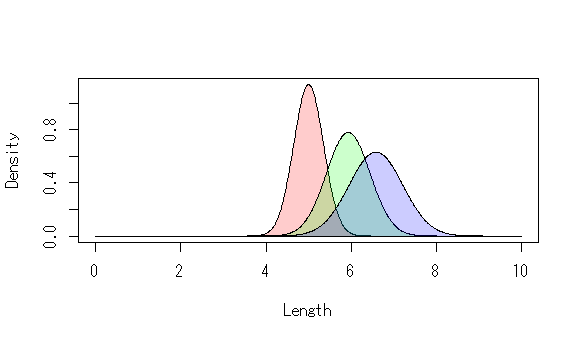
もちろん,標準偏差には影響を及ぼさないとか,標準偏差には影響を及ぼすけど,平均値には及ぼさない,といったモデルを作り,適合度を比較したり尤度比検定をしたりすることもできる。
まあでも,これ予測変数が因子型だったら,教師ありの混合分布モデルみたいなもん。
blmssパッケージでは,
m5<-bamlss(list(mu=iris[,1]~iris[,5],sigma=~iris[,5]),family="gaussian")
で,(当然だけど)同じような結果を得ることができる。MCMCサンプルを可視化したり,信用区間を構築してもよい。
とっても便利。
平均は変わらないけど,標準偏差だけ違う2群のモデル
回帰モデルは自由に作れるので,ある因子が標準偏差だけに影響を及ぼしているモデルとかも作れる。
たとえば,こんなデータだとしよう。
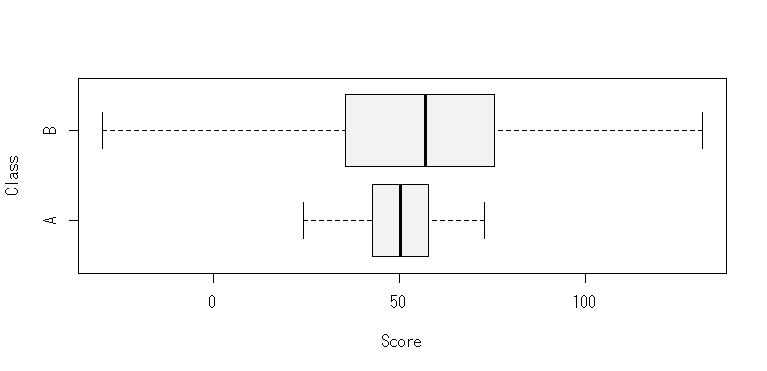
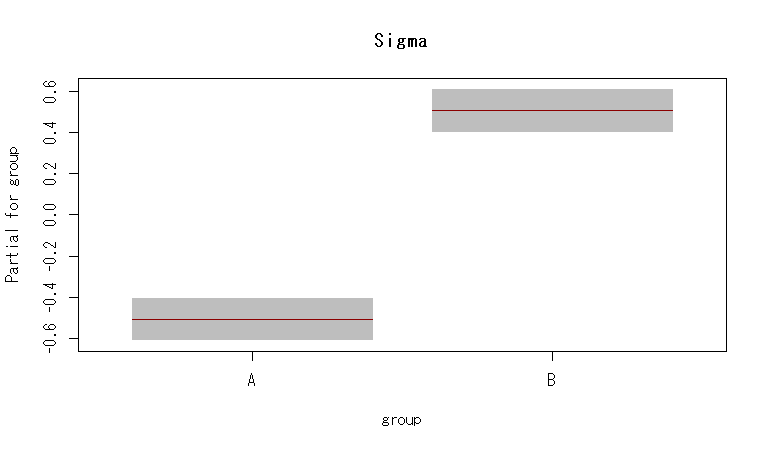
group<-as.factor(c(rep("A",100),rep("B",100))) score<-c(rnorm(100,50,10),rnorm(100,50,30)) d2<-data.frame(group,class) m6<-gamlss(score~1,sigma.formula=~group,data=d2) summary(m6) term.plot(m6,"sigma",main="Sigma")
結果はこんな感じ。
ちょっと複雑なモデル
えっと,実質的に意味があるかはわからないけど(ないだろう),がく片の長さの分布を正規分布だと仮定して,がく片の幅と花びらの長さから,その予測値という条件下における分布の母数(平均,標準偏差)を推定するとしよう。で,その予測値と予測される母数の関係は非線形だと。
#ここでは罰則付きスプラインの一種 m7<-gamlss(Sepal.Length~pb(Sepal.Width)+pb(Petal.Length),sigma.formula=~pb(Sepal.Width)+pb(Petal.Length),data=iris,family="NO") summary(m6) par(mfrow=c(2,2)) term.plot(m7,"mu",main="Mu") term.plot(m7,"sigma",main="Sigma")
可視化するとこんな感じ。
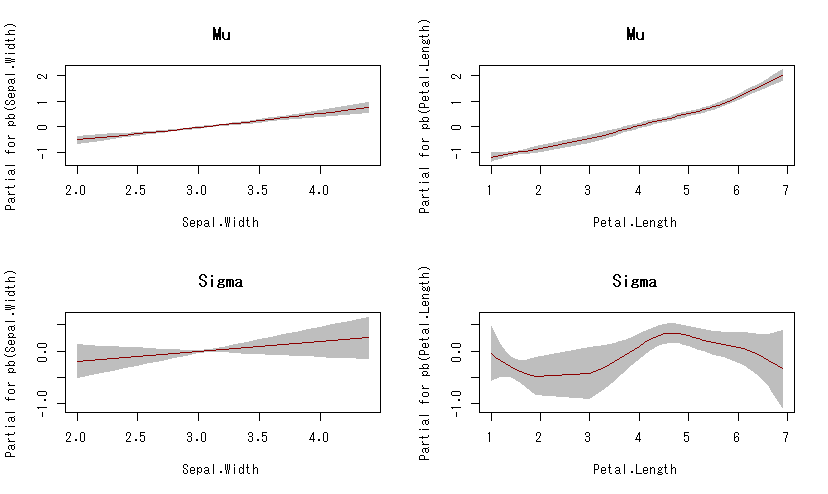
がく片の幅と花びらの長さが長くなれば,がく片の長さの分布における平均はそれぞれ単調に増加しそう(花びらの長さはちょっと指数的に見える)。
がく片の幅は,がく片の長さの分布における標準偏差とはあまり関係なさそうだ。しかし,花びらの長さは,がく片の長さの分布における標準偏差に非線形の影響を及ぼしているかも(意味ないと思うけど)。…みたいな。
で,これに種類を変量効果と考えて…というようにやっていくと,大分自由なモデリングができそう。
(最尤推定による分布のフィットから書き始めて,やっとここまで来たって感じ)
オンライン外国語学習における実測学習時間の格差:ジニ係数とローレンツ曲線
同じ学習教材を与えても,それを使用して勉強するひともいれば,勉強しないひともいる。格差,ということばが正しいかはわからないけど,たとえば大学生が,ある一定期間内において,大学が提供するオンライン外国語学習教材を使用して学習する時間は,ちょうど所得の分布に似た分布を示す。
これは歪んだ分布になる。(ワイブル分布の例;草薙(2017)は個人のWBTに対する個人のログイン時間は,ワイブル分布によって近似を与えられることを報告している)

これについて,ローレンツ曲線を描くとこんな感じ。

ちなみにこのデータのジニ係数は,だいたい0.30くらい。おおざっぱにいって,日本人の所得のジニ係数と同じくらい(?)。
全体のアクセス時間に対して,上半分の人が7割,下半分の人が3割の時間くらいといった比になる。下二割の人は,全体の7%,上8割の人の全体の93%。
この係数を減らすというのも,ひとつの業務的観点になりうる。
JansonとOllssonのイオタ
JansonとOllssonのイオタは,評定変数が多変量で複数評定者間の信頼性ないし一致率を評価する係数。Rでは,irrパッケージのiota関数を使う。
たとえばルーブリックを使用した評定を二人が行い,観点が5つあるとか,そんなときに使用する。
#こんなデータに [[1]] Rater1 Rater2 1 Old Old 2 New New 3 Old New 4 New New 5 Old Old 6 New New 7 New New 8 Old Old 9 New New [[2]] Rater1 Rater2 1 Slow Slow 2 Fast Fast 3 Slow Slow 4 Fast Fast 5 Slow Slow 6 Fast Fast 7 Slow Fast 8 Slow Slow 9 Fast Fast iota(dat)[] $method [1] "iota for nominal data (2 variables)" $subjects [1] 9 $raters [1] 2 $irr.name [1] "iota" $value [1] 0.775 $detail NULL
キーボード用リストレストを作ってしまえ
あまりタイピングが上手じゃないのがいけないのだけど,よく腱鞘炎になってしまう。私みたいにもの書きをまったくしないやつに限ってすぐ腱鞘炎になる。そんな軟弱な自分に嫌悪感を覚えながらも,やれキーボードが悪い,そしてリストレストが悪い,この企業の製品はダメだのと因果関係がそれほど自明でないことをいってしまうのが人間ってもの。本当は自分が軟弱なだけなのにね。自分の軟弱さを認めるくらいなら,顔の見えない製造企業を責めるほうが心が休まるものね。アマゾンのレビューもそういうのばっかり。
キーボードについても,世の人はやれメンブレンでも構わぬとか,パンタグラフで十分だの,メカニカルでないと死ぬ,それも赤軸がいいの,青軸がいいの,俺は黒軸でないと触らないだの,入門は茶軸がいいよとか,いいや無接点が最強だの,配列についてもUS配列でないとコードが書けないだとか日本人なんだから日本語配列でいこうぜとか,HHKBの配列でないとダメだとか,さらに細かいとControlはaの左だとかFnは右左に置けだとか,BSを一段下げろだとか矢印キーは甘えだとか,そもそもフルサイズキーボードがいいに決まっているとか,テンキーレスがいいだとか,いやいや60%コンパクトサイズがいいとか,もう開き直って40%キーボードでいいとか。
もはやリストレストでさえも,やれ幅は30cmがいいの奥行きは8cmがいいの,高さはどうのこうの,材質はどうの…
でもこれって難しい,自分は,HHKB Lite2 US配列と全く同じ配列で,フレームレスの赤軸(Minila ではいけない)が1万円きったら6台買おうと思う。しかしそういうのは存在しない。癖の強い自分みたいなものが欲しいものが企業にとって商機だとは限らない。
そうだ。なんか思い出した。そういえば,私が育った昭和時代の百姓の世界は,とても単純で複雑だった。なにか道具がほしければ,自分で作ったもんだった。なにか問題があれば,自分の工夫で解決したもんだった。さすがにキーボードは無理にしても,リストレストくらいだったら,誰でも簡単に自分で好きなように好きなだけ作れる。そうだ,仕様が気に入らないなら,仕様を責める前に自分で作ればいい。いつから俺は仕様を責めて自分ではなにも作らない人間になってしまったのか。
…というわけで,息抜きにキーボードのリストレストを作ってみることにした。
まずは家の近くのホームセンターにいって道具を集める。基本的にそれっぽい寸法の木材を買えばいい。自分の手には横30cm,奥行き8cm,高さは適当でいい,といって決めた。大概のホームセンターでは寸法を頼めば安く切ってくれるサービスがある。で,集めた材料とかはこんな感じ。
- 木材 30cm×8cm×5cm ×3 300円位
- 黒色スプレー
- やすり(持っている)
- サンドペーパー(100円)
- 木工用ボンド(100円)使わなかった
- すべり止めシート×3 300円

で,適当やすりで角を取って,適当にスプレーで黒く塗ると,どん。

おお,いいじゃないの。
で,裏にすべり止めシートを張ると,どん。

完成。20分くらい。技術も知識も手間もなにもいらない。

やば,高さよく考えてなかったから高すぎて到底使えないwwwww
高すぎるwwwww
あっれー!やっちまたー!
…次は高さもよく考えて作ろう。そうやって,トライアンドエラーで自分の好きな仕様を探っていこう。自分の手で作りながら。それって多分,とても単純で,そして心を捉える複雑なこと。
(続く)
左に歪んだデータへのフィッティング
確率分布のフィッティングでは,右に歪んだデータを対象にすることが多いのだけど,たまに左に歪んだ分布が手に入ることもある(てか私は最近はじめて手にいれた)。いろいろあるんだろうけど,一般化極値分布でいいかな。えっと,こんなデータだとしよう。

#準備とデータの作成 library(evd) library(fitdistrplus) library(ismev) library(MCMCpack) dat<-rgev(1000,20,3,-.5) hist(dat,main="",xlab="Value",breaks=20,col="pink") #まずはfitdist関数でフィット #初期値は適当に標本平均と標準偏差いれちゃう fit<-fitdist(dat,"gev",start=c(mean(dat),sd(dat),0)) summary(fit) Fitting of the distribution ' gev ' by maximum likelihood Parameters : estimate Std. Error 1 19.9521276 0.10240292 2 3.0110352 0.07695938 3 -0.4899288 0.01781197 Loglikelihood: -2398.873 AIC: 4803.746 BIC: 4818.469 Correlation matrix: [,1] [,2] [,3] [1,] 1.0000000 -0.2868652 -0.3588115 [2,] -0.2868652 1.0000000 -0.6712985 [3,] -0.3588115 -0.6712985 1.0000000 plot(fit)
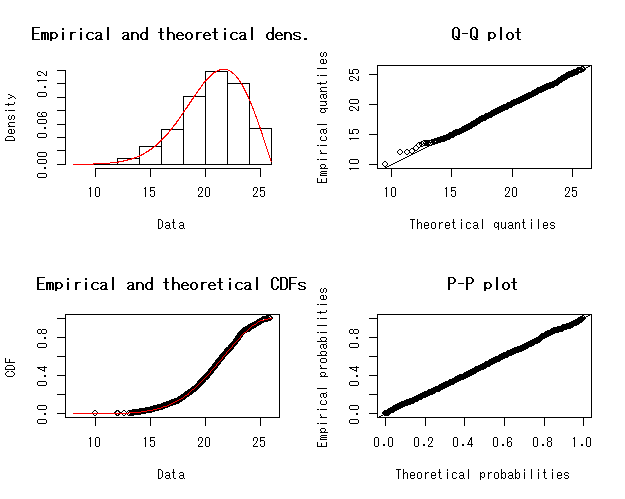
#ismevパッケージでフィット fit2<-gev.fit(dat) fit2 $conv [1] 0 $nllh [1] 2398.873 $mle [1] 19.9520718 3.0115839 -0.4900573 $se [1] 0.10241636 0.07699955 0.01780562 gev.diag(fit.gev)
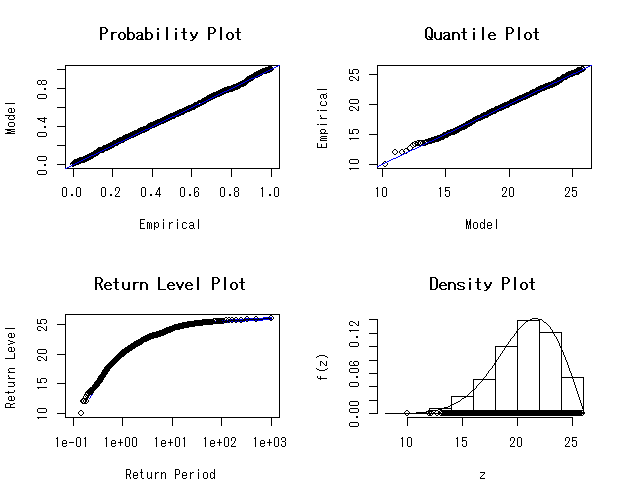
#無駄に無情報事前分布でMCMCしてみる llf<-function(beta,x){ sum(log(dgev(x,beta[1],beta[2],beta[3]))) } m<-MCMCmetrop1R(llf,theta.init=c(mean(dat),sd(dat),0),x=dat) summary(m) Iterations = 501:20500 Thinning interval = 1 Number of chains = 1 Sample size per chain = 20000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE [1,] 19.9413 0.10164 0.0007187 0.0024210 [2,] 3.0184 0.07621 0.0005389 0.0018702 [3,] -0.4871 0.01757 0.0001242 0.0004275 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% var1 19.7453 19.871 19.9407 20.0099 20.1407 var2 2.8700 2.966 3.0172 3.0689 3.1709 var3 -0.5214 -0.499 -0.4873 -0.4754 -0.4516 plot(m)

最尤法を使った逆ガウス分布のフィッティング
このブログへコメントがあったので,こちらで。
逆ガウス分布をデータに対して最尤法を使用してフィットする方法について。
statmodパッケージに逆ガウス分布の関数があって,それをfitdistrplusパッケージで使う。
#使うパッケージ library(statmod) library(fitdistrplus) #データの作成 dat<-rinvgauss(1000,1,4) #mu=1, lambda=4, n=1000の擬似乱数 #ヒストグラム hist(dat,col="lightblue", main="", xlab="value",freq=F,breaks=10,ylim=c(0,1.2)) #要約 summary(dat) #最尤推定 fit<-fitdist(dat,"invgauss",start=c(1,1)) #初期値をここではmu=1,lambda=1としている #結果 fit summary(fit) #Fitting of the distribution ' invgauss ' by maximum likelihood #Parameters : # estimate Std. Error #1 0.9950217 0.01505621 #2 4.3455699 0.19433979 #Loglikelihood: -520.8145 AIC: 1045.629 BIC: 1055.445 #だいたいよさげ #ヒストグラムに描き足し x<-seq(0,5,.01) lines(x,dinvgauss(x,fit$estimate[1],fit$estimate[2]),col="red",lty=2,lwd=3)
