わーい!どんなときでも有意差を見つけられるフレンズなんだね!
「思ったように有意差が出なかったんですけどなにかこのデータから言えることはありませんか?」
「どんなデザインですか?」
「処置群・統制群,事前・事後,成果変数は1です」
「そうですね…まずは処置群を恣意的に何パターンかに分割してみましょう!そうするとそれぞれのグループの標本サイズが減るし検定が多重になるので,事前事後の得点差について第一種の過誤の可能性が高まります!まあ4-5グループに分割したら,有意水準を補正しない限りどこか有意になるでしょう!これが王道です」
「はい!」
「その後に,さもそのパターン自体に最初から興味があったように研究仮説自体を改定するのです!これはHARKingと呼ばれる有名な技法です!」
「先生,大変です!性別,学年,事前の得点,学校,恋人の有無,そういった変数で分けたグループでも,どこにも有意はありません!」
「安心してください!まだ手はあります!今度は事前と事後で伸びたひと,伸びなかったひとの数を,手持ちの2値のデモグラフィック変数すべての組み合わせについてカイ二乗検定を別々にするのです!別々にやるのが大事ですよ!」
「先生ぇ…どこも有意になりません」
「大丈夫!まだ手はあります!外れ値だとして,事後得点の下側のひとりずつを外していき,それぞれのステップで何度も検定をして,有意になったときにやめてそれを報告するのです!」
「先生ぇ…ダメですぅ」
「そうですか,ではまず10個のデモグラフィック変数をすべて投入してクラスタリングをしましょう。まずは階層的クラスタリングを何回も繰り返して,有意になる階層でやめましょう。それでダメならクラスタリング方法を変えましょう。それでダメなら,k-means法,それでダメなら混合分布モデル,それでダメならクラスタリングに入れるデモグラフィック変数を減らしていきましょう。方法や,入れる変数の組み合わせで考えると無数にパターンができますから,どこかで必ず第一種の過誤が起きるはずです」
「先生ぇ…どうしましょう」
「(まじかそろそろ有意水準いじろっかな…)いえ!まだまだ手はあります。そもそも成果変数はなんですか?」
「英語のテストの点です」
「そうですか。項目数は?」
「30です」
「よかった,では項目分析をして,弁別力がなかったり信頼性を下げたりする項目をひとつずつ減らしてその度毎に検定をするのです!そして有意になったらやめるのです。なあに,その項目はなかったことにするか,materialのところにテストの質の観点から予め外したと書けばいいのですよ!もうなんなら全項目別々に検定したっていいくらいだ!」
「先生,外していったら項目がなくなりました…」
「(おいまじかよ)こんなことは数学的に絶対無いはずですが…ううむ」
「わたしはもうダメでしょうか…」
「大丈夫です!その被験者にまた来てもらって新しくテストをやりましょう!遅延テストといえばいいのです」
「…それはできなさそうです」
「では,どんなデータでもいいから被験者について知っていることはありませんでしたか」
「ええと,実験ノートに実験中あくびをした人をメモっておきました。靴下の色もメモってますよ!」
「素晴らしいですね!そのあくびをした数人を外して分析すると?」
「あ!あ!先生!有意です!やっと有意になりました!先生ありがとうございます!私の研究に有意差がありました!」
「わーい!有意差だ!先生はどんなときでも有意差を見つけられる先生なんですね!」
「たーのし―!」
*この記事はQRP(quetionable research practice)およびHARKing(研究仮説の改定),そして(本来するべきではない)事後的分析において無理に有意差を見出すことの悪質さについての理解を(私自身が)深めるために書いたものです。
モデルの中で何が捨象できるかを語らない科学
数理モデルというものは,その記述の仕方の形式性の割には,数理モデルということばに親しみを感じないほとんどのひとが思うより,本来結果主義的で効用主義的なものだ。
モデルは,もちろん現象それ自体ではないし,その現象を大幅に捨象していて,しかしそこから得られる予測や知見が有益だと見込まれているものだ。この「有益だ」という考え方は一部の学術分野にはないこともあるが。
人文社会系のほとんどの数理モデルは,世界が数字に支配されていて,その世界の斉一的な決定則を表すものだなんてことを意味しない。せいぜいが「観測がうまく当てはまる」,「うまい数理的な近似になっている」という程度の含意である。しかし,そのモデル(世界の決定則それ自体ではない)について考えることで,人が適切に意思決定をできたり,そして個人間の合意が得られ,判断の公共性が発生する(たとえばある種のエビデンスになる)というに考えられている。
たとえば,TOEICのスコアは大学が自前でやっている単語テストの成績から予測できるとする。
y = ax + b
という簡単なモデルを考えて,
TOEIC = 8.5×単語テストの得点 - 120
とか,そんなふうに。
このモデルは,それがうまくTOEICのスコアを予測できるとか,つまりこの現象のいい数理的な近似になっていれば,まあいいモデルだといえる。
ただし,このとき,TOEICは単語の力だけではないのだから,このモデルは世界の斉一的な決定則の記述として不完全だ!というのはちょっと勇み足だと思う。
TOEICは単語のテストだけではない!とか。
もっというなら,TOEICのときの部屋の温度をモデルに取り入れるべきかだとか,世界の斉一的な決定則を考えれば無限にそんな要因はありえる。
数理モデルを扱う人がもつ,結果主義というか,もっと大きくいってプラグマティズム的な考え方の下では,単にこのモデルはそれらを捨象しているのである。線形モデルなら,それら全部をひっくるめて誤差(残差)として考える。
ここで問題は,何が捨象できるかそして何を積極的に捨象するべきかということになる。
…外国語教育研究やその関連分野である第二言語習得研究が扱ってきた変数や現象は莫大であり,確かに複雑極まりない。もはや還元主義の傾向が強いテーマに関しては指数的に用語が増えていっていて,収拾付かない例もある。
だからこそ,なにが捨象できるか,そしてなにを捨象するべきか,という考えが今後重要になってくると思う。
そして個人的には,大局的に人間の意思決定や判断の合意形成や公共性の創出という点から見れば,捨象できるものはずっとずっと多いと思っている。
…世界の斉一的な決定則それ自体を考えるならば,むしろなにも捨象できないとも思っている。
Rで日付データの処理
自分用のメモ。
#日付クラスへ変換 d<-"2016-1-1" d2<-as.Date(d) class(d2) #日付データの足し引き(日付クラスだとこれができるようになるのが最高) d2-1 d2+1 d2-1000 d2+1000 #基準日から1日毎にログイン回数を累積計算 #datは時間とログイン回数のデータフレーム #基準日を設定 start<-as.Date("2016-04-08") r<-numeric(130) #計算 for(i in 1:130){ r[i]<-sum(dat[dat[,1]<start+i,2]) }
一般化パレート分布をデータに当てはめる
一般化パレート分布は所得の分布などに使われるそうだ。
外国語教育研究でもこういった分布になる変数を私はひとつだけ知っている(いわないwww)。
Rにいろいろあると思うけど,ここではactuarパッケージとfitdistrplusパッケージを使う。
actuarパッケージに関数があるから,それをfitdistrplusパッケージのfitdist関数当てはめるというわけ。
#パッケージの準備 library(actuar) library(fitdistrplus) #乱数作っちゃう #第一形状母数が3,第二形状母数が3,尺度母数が1000 set.seed(1) dat<-rgenpareto(1000,3,3,scale=1000) #経験分布を可視化 par(mfrow=c(1,2)) plot(ecdf(dat),main="") hist(dat,col="lightblue",main="")

#最尤推定(初期値は適当) fit<-fitdist(dat,"genpareto",start=list(shape1=1,shape2=1,scale=1000)) summary(fit) Fitting of the distribution ' genpareto ' by maximum likelihood Parameters : estimate Std. Error shape1 2.973575 0.3122382 shape2 2.811662 0.2800328 scale 1070.970526 236.9332116 Loglikelihood: -8230.236 AIC: 16466.47 BIC: 16481.2 Correlation matrix: shape1 shape2 scale shape1 1.0000000 -0.6723317 0.9114599 shape2 -0.6723317 1.0000000 -0.9020353 scale 0.9114599 -0.9020353 1.0000000 plot(fit)

うむ。
MCMCを使って指数正規合成分布(ex-Gaussian)の母数を推定
RのMCMCpackにはMCMCmetrop1Rっていう関数があって,これは任意(自作)の対数尤度の関数をいれてMCMCでサンプリングすることができる。なので,結構手軽にMCMCを使ってデータに好きな分布を当てはめることが可能。
ここでは(まったくそんなことはしなくてもいいんだけど),指数正規合成分布の母数(μ,σ,τ)をMCMCを使って推定してみる。
#準備 library(retimes) library(MCMCpack) #データの例 dat<-rexgauss(1000,3000,100,800) #関数の準備 llf<-function(beta,x){ sum(log(dexgauss(x,beta[1],beta[2],beta[3]))) } #MCMCしてみる,初期値は全部適当,burninとかmcmcの数とかデフォルトのまま m<-MCMCmetrop1R(llf,theta.init=c(2000,100,100),x=dat) #結果を見てみる summary(m) Iterations = 501:20500 Thinning interval = 1 Number of chains = 1 Sample size per chain = 20000 1. Empirical mean and standard deviation for each variable, plus standard error of the mean: Mean SD Naive SE Time-series SE [1,] 3005.7 13.00 0.09189 0.3102 [2,] 110.8 10.92 0.07724 0.2642 [3,] 779.5 27.79 0.19647 0.6677 2. Quantiles for each variable: 2.5% 25% 50% 75% 97.5% var1 2979.96 2997.0 3005.7 3014.3 3031.0 var2 90.49 103.5 110.5 117.8 133.7 var3 726.38 760.6 778.9 798.1 836.6 plot(m)

非線形最小二乗法で学習コンテンツ消化曲線をモデル化
まあ結構いろんなことに汎用的に当てはまることだと思うのだけど,ソフトウェアの品質管理とかの分野では,ソフトウェア信頼度成長曲線という手法があるそうだ(古い友人に教えてもらった)。
これは,ソフトウェア開発において,バグの発見数や残ったバグの数の予測などに使われるものだそうで,基本的には横軸に時間や工数,縦軸にはバグの数とかをプロットする。すると,S字カーブのような曲線になるそうだ。で,これを非線形最小二乗法を使って何かの関数に当てはめてモデル化するというはなし。ふむふむ。とっても面白そう。品質管理というだけあって,実用的だし,外国語教育の業務改善にもすごく通じるものがありそうだ。
外国語教育では,オンライン教材におけるコンテンツ消化率とかがパッと思いつくような例だ。オンライン教材で単語テストを繰り返すとか,そういう場面では,横軸に時間を,縦軸に消化率をプロットすると,おそらく同じように成長曲線を描くことができる。こんな感じだということしよう。ある学生があるオンライン教材を15週にかけて勉強した様子で,横軸には週,縦軸にはそのコンテンツの消化率をプロットした,と。(こういうデータは外国語教育にはかなりお蔵入りしてる)
#例の作成 t<-seq(1,15,1) d<-c(0.04,0.02,0.03,0.06,0.12,0.22,0.36,0.50,0.60,0.72,0.85,0.91,0.97,0.98,1.00) #作図 plot(t,d,xlab="時間(単位:週)",ylab="コンテンツ消化率")

このデータになんらかの関数を当てはめたい,と(最近欲求不満なのかなんでも当てはめたくなる)。
えっと,いろんな関数が当てはまるだろうけど,ここでは,ゴンペルツと4母数ロジスティック関数にしよう。
Rでやるには,デフォルトで使えるstatsパッケージのnlsという関数を使えばいい。非線形最小二乗法でフィッティングをする関数だ。いろいろ便利。
#ゴンペルツに当てはめ fit.gom<-nls(d~SSgompertz(t,Asym,b2,b3)) #結果 summary(fit.gom) Nonlinear regression model model: d ~ SSgompertz(t, Asym, b2, b3) data: parent.frame() Asym b2 b3 1.0985 12.1508 0.7114 residual sum-of-squares: 0.004886 Number of iterations to convergence: 0 Achieved convergence tolerance: 5.022e-06 AIC(fit.gom) BIC(fit.gom) #当てはめた曲線を描き足し plot(t,d,xlab="時間(単位:週)",ylab="コンテンツ消化率") lines(t,predict(fit.gom),lty=2,col=2) #4母数ロジスティック関数に当てはめ fit.fpl<-nls(d~SSfpl(t,A,B,xmid,scal)) #結果 summary(fit.fpl) Formula: d ~ SSfpl(t, A, B, xmid, scal) Parameters: Estimate Std. Error t value Pr(>|t|) A -0.009647 0.015871 -0.608 0.556 B 1.023469 0.017314 59.114 4.01e-15 *** xmid 8.223108 0.108640 75.692 2.66e-16 *** scal 1.791406 0.112481 15.926 6.06e-09 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.01943 on 11 degrees of freedom Number of iterations to convergence: 0 Achieved convergence tolerance: 3.818e-06 AIC(fit.fpl) BIC(fit.fpl) #当てはめた曲線をさらに描き足し plot(t,d,xlab="時間(単位:週)",ylab="コンテンツ消化率") lines(t,predict(fit.gom),lty=2,col=2) lines(t,predict(fit.fpl),lty=2,col=4) #2つのモデルをANOVA anova(fit.gom,fit.fpl) Analysis of Variance Table Model 1: d ~ SSgompertz(t, Asym, b2, b3) Model 2: d ~ SSfpl(t, A, B, xmid, scal) Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F) 1 12 0.0048859 2 11 0.0041547 1 0.00073119 1.9359 0.1916 #予測のために #ゴンペルツ曲線の関数を定義 gomf<-function(x,Asym,b2,b3){ y<-Asym*exp(-b2*b3^x) y } #4母数ロジスティック曲線の関数を定義 fplf<-function(x,A,B,xmid,scal){ y<-A+(B-A)/(1+exp((xmid-x)/scal)) y }
この例だとピッタシだ。

外国語教育研究では,これと似たような技術の応用に,キーログを使った川口ほか(2016, Language Education & Technology)がある。
CiNii 論文 - エッセイライティングにおける増加語数の時系列推移傾向とエッセイ評価の関係 : モデルフィッティングを用いた検討
混合正規指数合成分布モデル(?)を最尤法で…
聞いたこともないけど,要素数2の混合正規指数合成分布(ex-Gaussian)モデルというのを考えてみる。ま,2つの異なる認知プロセスが混合したときの反応時間の分布だとか,そんなそれっぽいことを考えてみる。そんなものは多分ない。
ま,でもこの確率密度関数は,
dmixexgauss<-function(x,lambda,mu1,sigma1,tau1,mu2,sigma2,tau2){ y<-lambda*(1/tau1)*exp(mu1/tau1+(sigma1^2)/(2*tau1^2)-x/tau1)* pnorm(x,mu1+(1/tau1)*sigma1^2, sigma1) +(1-lambda)*(1/tau2)*exp(mu2/tau2+(sigma2^2)/(2*tau2^2)-x/tau2)* pnorm(x,mu2+(1/tau2)*sigma2^2,sigma2) return(y) }
こうなはず。これで尤度関数を作って,bbmleパッケージのmle2とかで最尤推定してみれば…と思ったんだけど,やっぱ上手く推定できなかった。methodもBFGSとかいろいろ試したけど,ううむ。なんと7母数の確率密度関数だもんな。俺の間違いってのもあるし。
ま,でもこの自作の確率密度関数自体はあってるぽい。暇ができたらちょっとやってみよう。
library(retimes) set.seed(1) dat<-c(rexgauss(400,1000,300,800),rexgauss(100,4000,800,500)) hist(dat,main="",breaks=20,col="lightblue",freq=F,ylim=c(0,.0006),xlim=c(0,8000)) x<-seq(0,8000,1) lines(x,dmixexgauss(x,.80,1000,300,800,4000,800,500),lty=2,col=2)
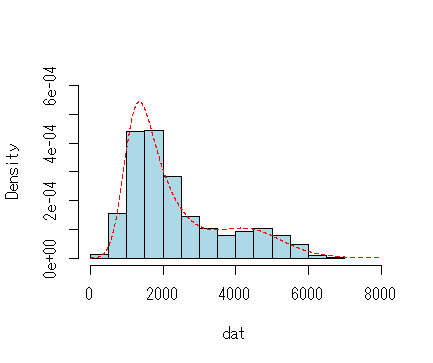
*追記(1/28)
標本サイズ,母数,初期値次第では結構うまくいく場合もあるようだ。たとえば,
#あからさまな例 set.seed(1) dat<-c(rexgauss(500,1000,500,100),rexgauss(500,10000,500,100)) #mle2で最尤推定 #対数尤度を返す関数 lf<-function(l,m1,s1,t1,m2,s2,t2){ -sum(log(dmixexgauss(dat,l,m1,s1,t1,m2,s2,t2))) } #適当な初期値で最尤推定 fit<-mle2(lf,start=list(l=.01,m1=1000,s1=100,t1=100,m2=10000,s2=100,t2=100)) summary(fit) Maximum likelihood estimation Call: mle2(minuslogl = lf, start = list(l = 0.01, m1 = 1000, s1 = 100, t1 = 100, m2 = 10000, s2 = 100, t2 = 100)) Coefficients: Estimate Std. Error z value Pr(z) l 5.0001e-01 1.5811e-02 31.6234 < 2.2e-16 *** m1 8.8352e+02 5.3678e+01 16.4598 < 2.2e-16 *** s1 4.2277e+02 2.8256e+01 14.9618 < 2.2e-16 *** t1 2.5258e+02 5.1428e+01 4.9114 9.043e-07 *** m2 9.8383e+03 5.6083e+01 175.4242 < 2.2e-16 *** s2 4.4467e+02 2.8829e+01 15.4245 < 2.2e-16 *** t2 2.4854e+02 5.3408e+01 4.6536 3.263e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 -2 log L: 16646.24 coef(fit) vcov(fit) AIC(fit)